Question

6．已知正方形ABCD中，AB=BC=CD=DA=4，∠A=∠B=∠C=∠D=90°．动点P以每秒1个单位速度从点B出发沿线段BC方向运动，动点Q同时以每秒4个单位速度从A点出发沿正方形的边AD-DC-CB方向顺时针作折线运动，当点P与点Q相遇时停止运动，设点P的运动时间为t．
（1）当运动时间为$\frac{12}{5}$ 秒时，点P与点Q相遇；
（2）当AP∥CQ时，求线段DQ的长度；
（3）用含t的代数式表示以点Q、P、A为顶点的三角形的面积S，并指出相应t的取值范围；
（4）连接PA，当以点Q及正方形的某两个顶点组成的三角形和△PAB全等时，求t的值．

Answer 1

分析 （1）设t秒后P、Q相遇．列出方程即可解决问题．
（2）如图1中，AP∥QC时，由AQ∥PC，推出四边形APCQ是平行四边形，根据AQ=PC，列出方程即可解决问题．
（3）分三种情形①如图2中，当0＜t≤1，点Q在AD上时．②如图3中，当1＜t≤2，点Q在CD上时，S=S_{正方形ABCD}-S_△ADQ-S_△ABP-S_△PQC．③如图4中，当2＜t≤$\frac{12}{5}$，点Q在BC时时．分别求解即可．
（4）分四种情形求解①当DQ₁=BP时，△CDQ₁≌△ABP．②当DQ₂=BP时，△ADQ₂≌△ABP．③当CQ₃=BP时，△BCQ₃≌△ABP．④当BQ₄=BP时，△ABQ₄≌△ABP，此时P与Q重合．

解答 解：（1）设t秒后P、Q相遇．
由题意（4+1）t=12，
∴t=$\frac{12}{5}$秒，
∴$\frac{12}{5}$秒后P、Q相遇．
故答案为$\frac{12}{5}$．

（2）如图1中，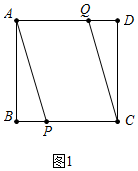

由图象可知，AP∥QC时，∵AQ∥PC，
∴四边形APCQ是平行四边形，
∴AQ=PC，
∴4t=4-t，
∴t=$\frac{4}{5}$，此时DQ=AD-AQ=4-$\frac{4}{5}$×4=$\frac{4}{5}$．

（3）①如图2中，当0＜t≤1，点Q在AD上时，S=$\frac{1}{2}$×4t×4=8t．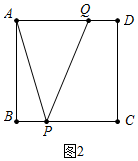

②如图3中，当1＜t≤2，点Q在CD上时，S=S_{正方形ABCD}-S_△ADQ-S_△ABP-S_△PQC=16-$\frac{1}{2}$×4×（4t-4）-$\frac{1}{2}$×4×t-$\frac{1}{2}$×（4-t）（8-4t）=-2t²+2t+8．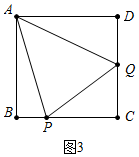

③如图4中，当2＜t≤$\frac{12}{5}$，点Q在BC时时，S=$\frac{1}{2}$×[4-t-（4t-8）]•4=-10t+24．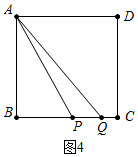

综上所述，S=$\left\{\begin{array}{l}{8t}&{（0＜t≤1）}\\{-2{t}^{2}+2t+8}&{（1＜t≤2）}\\{-10t+24}&{（2＜t≤\frac{12}{5}）}\end{array}\right.$．

（4）如图5中，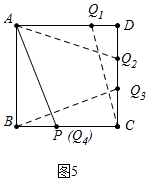

①当DQ₁=BP时，△CDQ₁≌△ABP，此时4-4t=t，t=$\frac{4}{5}$s．
②当DQ₂=BP时，△ADQ₂≌△ABP，此时4t-4=t，t=$\frac{4}{3}$s．
③当CQ₃=BP时，△BCQ₃≌△ABP，此时8-4t=t，t=$\frac{8}{5}$s．
④当BQ₄=BP时，△ABQ₄≌△ABP，此时P与Q重合，t=$\frac{12}{5}$s
综上所述，t为$\frac{4}{5}$s或$\frac{4}{3}$s或$\frac{8}{5}$s或$\frac{12}{5}$s时，当以点Q及正方形的某两个顶点组成的三角形和△PAB全等．

点评 本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会分类讨论，注意不能漏解，属于中考压轴题．