
【题目】已知正比例函数和反比例函数的图象都经过点 A(3,3).
(1)求正比例函数和反比例函数的解析式;
(2)把直线 OA 向下平移后得到直线 l,与反比例函数的图象交于点 B(6,m),求 m 的值和直线 l 的解 析式;
(3)在(2)中的直线 l 与 x 轴、y 轴分别交于 C、D,求四边形 OABC 的面积.

【答案】(1)正比例函数的解析式为y=x,反比例函数的解析式为y=![]() ; (2)直线l的解析式为y=x
; (2)直线l的解析式为y=x![]() ; (3)S四边形OABC=
; (3)S四边形OABC=![]() .
.
【解析】
(1)利用待定系数法,由正比例函数和反比例函数的图象都经过点A(3,3),即可求得解析式;
(2)由点B在反比例函数图象上,即可求得m的值;又由此一次函数是正比例函数平移得到的,可知一次函数与反比例函数的比例系数相同,代入点B的坐标即可求得解析式;
(3)构造直角梯形AEFD,则通过求解△ABE、△BDF与直角梯形ADFE的面积即可求得△ABD的面积.
(1)设正比例函数的解析式为y=ax,反比例函数的解析式为y=![]() ,
,
∵正比例函数和反比例函数的图象都经过点A(3,3),
∴3=3a,3=![]() ,
,
∴a=1,b=9,
∴正比例函数的解析式为y=x,反比例函数的解析式为y=![]() ;
;
(2)∵点B在反比例函数上,
∴m=![]() =
=![]() ,
,
∴B点的坐标为(6,![]() ),
),
∵直线BD是直线OA平移后所得的直线,
∴可设直线BD的解析式为y=x+c,
∴![]() =6+c,
=6+c,
∴c=![]() ,
,
∴直线l的解析式为y=x![]() ;
;

(3)过点A作AE∥x轴,交直线l于点E,连接AC.
∵直线l的解析式为y=x![]() ,A(3,3),
,A(3,3),
∴点E的坐标为(![]() ,3),点C的坐标为(
,3),点C的坐标为(![]() ,0).
,0).
∴AE=![]() 3=
3=![]() ,OC=
,OC=![]() ,
,
∴S四边形OABC=S△OAC+S△ACES△ABE=![]() ×
×![]() ×3+
×3+![]() ×
×![]() ×3
×3![]() ×
×![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
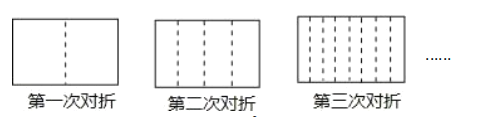
【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到![]() 条折痕,那么对折四次可以得到( )条折痕.如果对折
条折痕,那么对折四次可以得到( )条折痕.如果对折![]() 次, 可以得到( )条折痕
次, 可以得到( )条折痕
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芭蕾舞剧《吉赛尔》在城市剧院演出前,主办方工作人员准备利用![]() 米长的墙为一边,用
米长的墙为一边,用![]() 米隔栏绳作为另三边,设立一个面积为
米隔栏绳作为另三边,设立一个面积为![]() 平方米的长方形等候区,如图,为了方便观众进出,在与墙垂直的两边上留出一个进口和两个出口,宽度都为
平方米的长方形等候区,如图,为了方便观众进出,在与墙垂直的两边上留出一个进口和两个出口,宽度都为![]() 米,问围成的这个长方形的相邻两边长分别是多少?
米,问围成的这个长方形的相邻两边长分别是多少?

解:令这个长方形垂直于墙的一边为宽,平行于墙的一边为长;设这个长方形的宽为![]() 米,则长为_____________米.(完成填空后继续解题)
米,则长为_____________米.(完成填空后继续解题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,菱形 ABOC 的顶点 O 在坐标原点,边 BO 在 x 轴的负半轴上,顶点 C的坐标为(﹣3,4),反比例函数 y ![]() 的图象与菱形对角线 AO 交于 D 点,连接 BD,当 BD⊥x 轴时,k的值是( )
的图象与菱形对角线 AO 交于 D 点,连接 BD,当 BD⊥x 轴时,k的值是( )

A.![]() B.
B.![]() C.﹣12D.
C.﹣12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点 A 是反比例函数 y ![]() 在第一象限图象上的一个动点,连接 OA,以
在第一象限图象上的一个动点,连接 OA,以![]() OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y
OA 为长,OA为宽作矩形 AOCB,且点 C 在第四象限,随着点 A 的运动,点 C 也随之运动,但点 C 始终在反比例函数 y ![]() 的图象上,则 k 的值为________.
的图象上,则 k 的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,
是角平分线,![]() ,
,![]() .
.

(![]() )求
)求![]() 、
、![]() 和
和![]() 的度数.
的度数.
(![]() )若图形发生了变化,已知的两个角度数改为:当
)若图形发生了变化,已知的两个角度数改为:当![]() ,
,![]() ,则
,则![]() __________
__________![]() .
.
当![]() ,
,![]() 时,则
时,则![]() __________
__________![]() .
.
当![]() ,
,![]() 时,则
时,则![]() __________
__________![]() .
.
当![]() ,
,![]() 时,则
时,则![]() __________
__________![]() .
.
(![]() )若
)若![]() 和
和![]() 的度数改为用字母
的度数改为用字母![]() 和
和![]() 来表示,你能找到
来表示,你能找到![]() 与
与![]() 和
和![]() 之间的关系吗?请直接写出你发现的结论.
之间的关系吗?请直接写出你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
利用完全平方公式,可以将多项式ax2+bx+c(a≠0)变形为a(x+m)2+n的形式,我们把这样的变形方法叫做多项式ax2+bx+c的配方法.
运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:x2+11x+24=![]()
=![]()
=![]()
=(x+8)(x+3)
根据以上材料,解析下列问题:
(1)用多项式的配方法将x2+8x﹣1化成(x+m)2+n的形式;
(2)求证:x,y取任何实数时,多项式x2+y2﹣2x﹣4y+16的值总为正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,AE平分∠BAC.
(1)若∠B=30°,∠C=70°,则∠DAE=
(2)若∠C﹣∠B=30°,则∠DAE= .
(3)若∠C﹣∠B=α(∠C>∠B),求∠DAE的度数(用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xoy 中,已知点 A 的坐标为(-2,0).
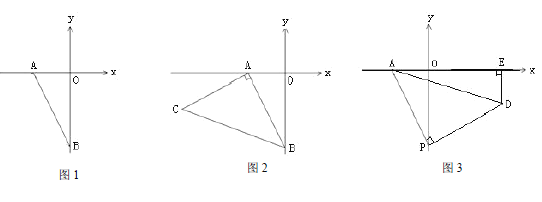
(1)如图 1,当点 B 的坐标为(0,-4)时,则△AOB 的面积是 ;
(2)如图 2,在(1)的条件下,过点 A 作 AC⊥AB,且使 AC=AB,求第三象限内的点 C 的坐标;
(3)如图 3,P 为 y 轴负半轴上一点,过点 P 作 PD⊥PA,且使 PD=PA,过第四象限内的点 D 作 DE⊥x 轴于 E,试判断 OP-DE 的值是否发生变化.若不发生变化,请求其值;若发生变化,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com