
分析 (1)直接利用幂的乘方运算法则计算即可;
(2)直接利用幂的乘方运算法则结合同底数幂的乘除法运算法则计算即可;
(3)直接利用幂的乘方运算法则结合积的乘方运算法则计算即可;
(4)直接利用同底数幂的乘法运算法则计算即可;
(5)直接利用幂的乘方运算法则结合积的乘方运算法则、合并同类项计算即可;
(6)直接利用零指数幂的性质结合负指数幂的性质、绝对值的性质分别化简求出答案.
解答 解:(1)(-m)12•(-m)5
=-m12•m5
=-m17;
(2)a2•a4+(a3)2
=a6+a6
=2a6;
(3)(-a3)2•(-a2)3
=-a6•a6
=-a12;
(4)(p-q)4•(q-p)3•(p-q)2
=(p-q)9;
(5)(-2x2)3+x2•x4-(-3x3)2
=-8x6+x6+9x6
=2x6;
(6)|-1|+(-2)3+(7-π)0-($\frac{1}{3}$)-1
=1-8+1-3
=-9.
点评 此题主要考查了幂的乘方运算、同底数幂的乘法运算以及实数运算等知识,正确掌握运算法则是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
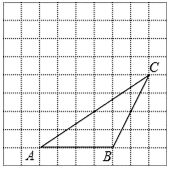 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com