
【题目】阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如![]() 是方程
是方程![]() 的一个解,对应点
的一个解,对应点![]() ,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点
,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点![]() 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程
将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程![]() 的解.所以,我们就把条直线就叫做方程
的解.所以,我们就把条直线就叫做方程![]() 的图象.
的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知![]() 、
、![]() 、
、![]() ,则点__________(填“A或
,则点__________(填“A或![]() 或
或![]() ”)在方程
”)在方程![]() 的图象上.
的图象上.
(2)求方程![]() 和方程
和方程![]() 图象的交点坐标.
图象的交点坐标.
(3)已知以关于![]() 的方程组
的方程组![]() 的解为坐标的点在方程
的解为坐标的点在方程![]() 的图象上,当
的图象上,当![]() 时,化简
时,化简![]() .
.

科目:初中数学 来源: 题型:
【题目】某工厂计划生产![]() 两种产品共10件,其生产成本和销售价如下表所示:
两种产品共10件,其生产成本和销售价如下表所示:
产品 |
|
|
成本(万元/件) | 3 | 5 |
售价(万元/件) | 4 | 7 |
(1)若工厂计划获利14万元,则应分别生产![]() 两种产品多少件?
两种产品多少件?
(2)若工厂投入资金不多于44万元,且获利不少于14万元,则工厂有哪些生产方案?
(3)在第(2)的条件下,哪种方案获利最大;最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
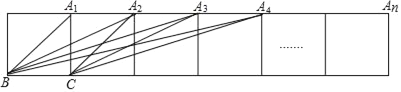
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是8×8的标准点阵图,直线l、m互相垂直,已知△ABC.

(1)写出△ABC的形状;
(2)分别画出△ABC关于直线l、m对称的△A1B1C1,△A2B2C2,再画出△A1B1C1关于直线m对称的△A3B3C3
(3)△A2B2C2与△A3B3C3关于哪条直线对称? (填“直线l、m”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
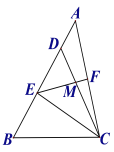
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
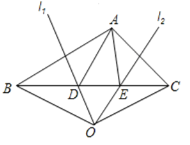
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(6,0),B(8,5),将线段OA平移至CB,点D(x,0)在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)△ODC与△ABD的面积分别记为S1,S2,设S=S1﹣S2,求S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等,如果存在,请求出x的值(或取值范围);如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com