
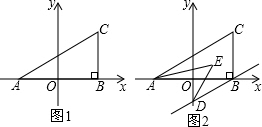
分析 (1)根据非负数的性质求出a、b,根据三角形的面积公式计算即可;
(2)作EH∥AC,根据平行线的性质得到∠ABD=∠CAB,得到∠CAB+∠ODB=90°,根据角平分线的定义、平行线的性质计算即可;
(3)根据三角形中位线定理求出OD,设点P的坐标为:(0,y),根据三角形的面积公式列出方程,解方程即可.
解答 解:(1)由题意得,a+2=0,b-2=0,
解得,a=-2,b=2,
则A(-2,0),C(2,2),
∴AB=2+2=4,BC=2,
则△ABC的面积=$\frac{1}{2}$×AB×BC=4;
(2)如图2,作EH∥AC,
∵BD∥AC,
∴BD∥EH,
∵BD∥AC,
∴∠ABD=∠CAB,
∴∠CAB+∠ODB=90°,
∵AE、DE分别平分∠CAB、∠ODB,
∴∠CAE=$\frac{1}{2}$∠CAB,∠EDB=$\frac{1}{2}$∠ODB,
∴∠CAE+∠EDB=45°,
∵EH∥AC,BD∥EH,
∴∠AEH=∠CAE,∠DEH=∠EDB,
∴∠AED=∠AEH+∠DEH=45°;
(3)由三角形中位线定理得,OD=$\frac{1}{2}$BC=1,
设点P的坐标为:(0,y),
S△ACP=S△ADP+S△CDP
由题意得,$\frac{1}{2}$×|y-1|×2+$\frac{1}{2}$×|y-1|×2=4,
解得,y=3或-1,
答:△ABC和△ACP的面积相等时,P点坐标为(0,3)或(0,-1).
点评 本题考查的是相似三角形的判定和性质、非负数的性质、角平分线的定义,掌握相似三角形的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | ||
| C. | 对角线相等的任意四边形 | D. | 对角线垂直的任意四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-1)^{2}}$=-1 | B. | ±$\sqrt{16}$=±4 | C. | $(\sqrt{5})^{2}$=25 | D. | $\root{3}{-27}$=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com