
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .已知抛物线
.已知抛物线![]() (
(![]() 是常数),顶点为
是常数),顶点为![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求顶点
时,求顶点![]() 的坐标;
的坐标;
(Ⅱ)若点![]() 在
在![]() 轴下方,当
轴下方,当![]() 时,求抛物线的解析式;
时,求抛物线的解析式;
(Ⅲ) 无论![]() 取何值,该抛物线都经过定点
取何值,该抛物线都经过定点![]() .当
.当![]() 时,求抛物线的解析式.
时,求抛物线的解析式.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 或
或![]() .
.
【解析】(Ⅰ)把点A(1,0)代入![]() 求出m的值,从而确定二次函数解析式,进而求出顶点P的坐标;
求出m的值,从而确定二次函数解析式,进而求出顶点P的坐标;
(Ⅱ)先由函数解析式得出顶点坐标为![]() .再结合已知条件可知
.再结合已知条件可知![]() ,从而求出
,从而求出![]() ,
,![]() .再进行分类讨论得到抛物线解析式为
.再进行分类讨论得到抛物线解析式为![]() ;
;
(Ⅲ)由![]()
![]() 可知,定点H的坐标为
可知,定点H的坐标为![]() ,过点
,过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,则可证
,则可证![]() .得点
.得点![]() 的坐标为
的坐标为![]() 或
或![]() .然后进行分类讨论即可求解.
.然后进行分类讨论即可求解.
(Ⅰ)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为![]() .
.
∵![]()
![]() ,
,
∴顶点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)抛物线![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
由点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴下方,
轴下方,![]() ,知点
,知点![]() 在第四象限.
在第四象限.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
可知![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 不在第四象限,舍去.
不在第四象限,舍去.
∴![]() .
.
∴抛物线解析式为![]() .
.
(Ⅲ)由![]()
![]() 可知,
可知,
当![]() 时,无论
时,无论![]() 取何值,
取何值,![]() 都等于4.
都等于4.
得点![]() 的坐标为
的坐标为![]() .
.
过点![]() 作
作![]() ,交射线
,交射线![]() 于点
于点![]() ,分别过点
,分别过点![]() ,
,![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .∴
.∴![]() .
.
∵![]()
![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
可得点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,可得直线
时,可得直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在直线
在直线![]() 上,
上,
∴![]() .解得
.解得![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 与点
与点![]() 重合,不符合题意,∴
重合,不符合题意,∴![]() .
.
当点![]() 的坐标为
的坐标为![]() 时,
时,
可得直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在直线
在直线![]() 上,
上,
∴![]()
![]() .解得
.解得![]() (舍),
(舍),![]() .
.
∴![]() .
.
综上,![]() 或
或![]() .
.
故抛物线解析式为![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
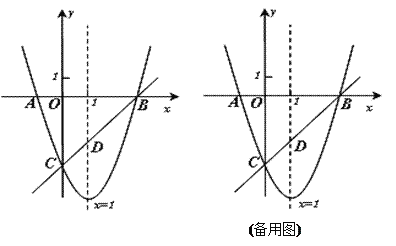
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
⑴求抛物线的函数表达式;
⑵求直线BC的函数表达式;
⑶点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段PQ=![]() AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一些蜂蜜,此时一只蚂蚁正好也在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,那么蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离是( )

A.13B.14C.15D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
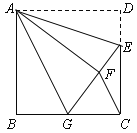
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区要在一块长方形的空地上修建三条人行道(阴影部分),其余空地铺设草坪进行美化,设计规划如图所示,长方形空地长为m米,宽为n米,且三条人行道宽均为2米.
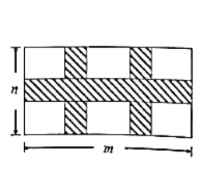
(1)请直接写出草坪面积是多少平方米?(用m,n表示)
(2)若n=18,且人行道所占面积为整个长方形空地面积的![]() ,则该长方形空地的长为多少米?
,则该长方形空地的长为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
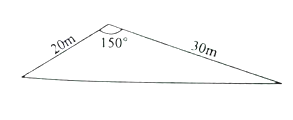
【题目】我市在旧城改造中,计划在市内一块如下图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价![]() 元,则购买这种草皮至少需要______元.
元,则购买这种草皮至少需要______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com