
【题目】如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(3,0)两点,点C是抛物线与y轴的交点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;
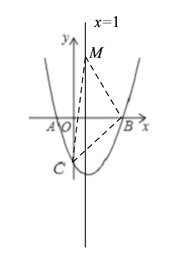
(3)在抛物线的对称轴上是否存在点M,使△BCM是等腰三角形,若存在请直接写出点M坐标,若不存在请说明理由.
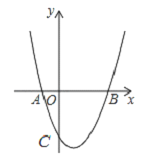
【答案】(1) y=x2﹣2x﹣3,顶点坐标为(1,﹣4).(2) ﹣4≤y<0;(3)存在, 点M的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,-1).
)或(1,-1).
【解析】试题分析:
(1)把点A、B的坐标代入y=x2+bx+c中,列方程组解得b、c的值即可得到抛物线的解析式;把所得解析式配方化为“顶点式”可得顶点坐标;
(2)根据(1)中所得抛物线的顶点坐标和点B的坐标结合图形可得本题答案;
(3)设点M的坐标为(1,m),由两点间距离公式(或勾股定理),表达出:CB2、CM2、BM2,再分①CB2=CM2;②CB2=BM2;③CM2=BM2三种情况分别列出关于“m”的方程,解方程即可可得到答案.
试题解析:
(1)把A(﹣1,0)、B(3,0)分别代入y=x2+bx+c中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线顶点坐标为(1,﹣4).
(2)∵在y=x2﹣2x﹣3中,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ;抛物线顶点坐标为(1,-4),
;抛物线顶点坐标为(1,-4),
∴当0<x<3时, ![]() 的取值范围为:﹣4≤y<0;.
的取值范围为:﹣4≤y<0;.
(3)存在.由(1)和(2)可知,抛物线的对称轴为直线![]() ,点C的坐标为(0,-3),
,点C的坐标为(0,-3),
∴可设点M的坐标为(1,m),由此可得:CB2=18;CM2=![]() ;BM2=
;BM2=![]() .
.
①当CB2=CM2时,有![]() ,解得:
,解得: ![]() ;
;
②当CB2=BM2时,有![]() ,解得:
,解得: ![]() ;
;
③当CM2=BM2时,有![]() ,解得:
,解得: ![]() ;
;
综上所述,存在点M使△BCM是等腰三角形,M的坐标为: ![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.


科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
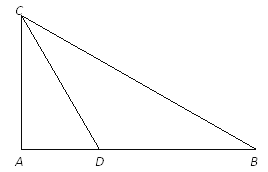
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,港口A位于灯塔C的正南方向,港口B位于灯塔C的南偏东60°方向,且港口B在港口A的正东方向的135公里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯塔C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时到达港口B,顺利完成交货.求货轮原来的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
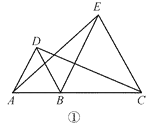
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
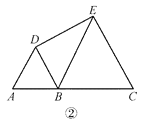
(2)如图②,若 AB=1,BC=2,求 DE 的长;
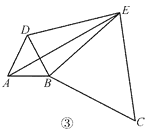
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%.
(1)这种商品A的进价为多少元?
(2)现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com