练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （2012•湘潭）如图，在?ABCD中，点E在DC上，若EC：AB=2：3，EF=4，则BF=
    6
    6
    ．
    分析：先根据平行四边形的性质得出∠CAB=∠ACD，∠ABE=∠BEC，故可得出△ABF∽△CEF，再由相似三角形的对应边成比例即可得出结论．
    解答：解：∵四边形ABCD是平行四边形，
    ∴AB∥CD，
    ∴∠CAB=∠ACD，∠ABE=∠BEC，
    ∴△ABF∽△CEF，
    ∴
    AB
    CE
    =
    BF
    EF
    ，即
    3
    2
    =
    BF
    4
    ，解得BF=6．
    故答案为：6．
    点评：本题考查的是相似三角形的判定与性质，熟知相似三角形的判定定理是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2012•湘潭）如图，在⊙O中，弦AB∥CD，若∠ABC=40°，则∠BOD=（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•湘潭）如图，抛物线y=ax2-
    32
    x-2(a≠0)    的图象与x轴交于A、B两点，与y轴交于C点，已知B点坐标为（4，0）．
    （1）求抛物线的解析式；
    （2）试探究△ABC的外接圆的圆心位置，并求出圆心坐标；
    （3）若点M是线段BC下方的抛物线上一点，求△MBC的面积的最大值，并求出此时M点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•湘潭）如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•湘潭）如图，△ABC的一边AB是⊙O的直径，请你添加一个条件，使BC是⊙O的切线，你所添加的条件为
    ∠ABC=90°
    ∠ABC=90°
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

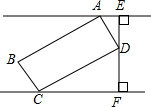    （2012•湘潭）如图，矩形ABCD是供一辆机动车停放的车位示意图，已知BC=2m，CD=5.4m，∠DCF=30°，请你计算车位所占的宽度EF约为多少米？（
    		3
    ≈1.73    ，结果保留两位有效数字．）

    查看答案和解析>>

    同步练习册答案