
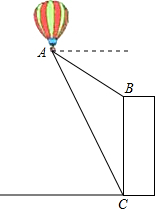
 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°.热气球A的高度为240米,求这栋大楼的高度.
如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°.热气球A的高度为240米,求这栋大楼的高度.科目:初中数学 来源: 题型:
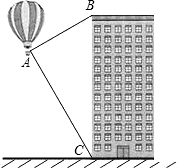 如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
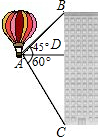 如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,求这栋楼的高度.(| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
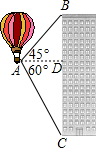 如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,则这栋楼的高度为
如图,热气球的探测器显示,从热气球看一栋高楼的顶部B的仰角为45°,看这栋高楼底部C的俯角为60°,热气球与高楼的水平距离AD为50m,则这栋楼的高度为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
(2013•德阳)如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )查看答案和解析>>
科目:初中数学 来源: 题型:
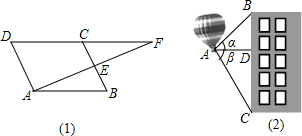 (2012•福州质检)(1)如图,在平行四边形ABCD中,E为BC中点,AE和延长线与DC的延长线相交于点F.证明:△ABE≌△FCE.
(2012•福州质检)(1)如图,在平行四边形ABCD中,E为BC中点,AE和延长线与DC的延长线相交于点F.证明:△ABE≌△FCE.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com