
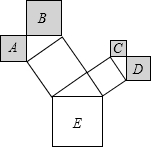
 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是2,3,1,2,则最大正方形E的面积是18.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是2,3,1,2,则最大正方形E的面积是18.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
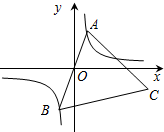 如图,已知:点A是双曲线y=$\frac{3}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$ (x>0)上运动,则k的值是-9.
如图,已知:点A是双曲线y=$\frac{3}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$ (x>0)上运动,则k的值是-9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
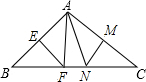 如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.
如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
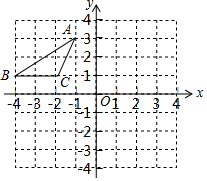 如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
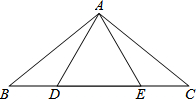 如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,请你添加一个条件使∠DAB=∠EAC.
如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,请你添加一个条件使∠DAB=∠EAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com