
分析 (1)根据反比例函数图象上点的坐标特征,设公共点的坐标为($\frac{a-3}{4}$,4),然后把($\frac{a-3}{4}$,4)代入y=(a+3)x=4得到关于a的方程,然后解方程求出a即可得到一次函数和反比例函数的解析式;
(2)利用描点法画出两函数图象;
(3)利用函数图象,写出反比例函数图象在一次函数图象上方所对应的自变量的范围即可.
解答 解:(1)设公共点的坐标为($\frac{a-3}{4}$,4),
把($\frac{a-3}{4}$,4)代入y=(a+3)x=4得$\frac{a-3}{4}$•(a+3)=4,解得a1=5,a2=-5,
而a<0,
所以a=-5,
所以一次函数解析式为y=-2x,反比例函数解析式为y=-$\frac{8}{x}$;
(2)如图,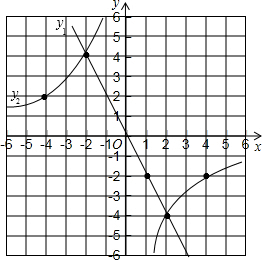
(3)当-2<x<0或x>2时,y1<y2.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点问题(1)求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
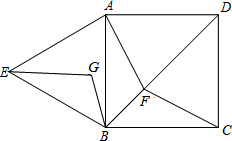 已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.
已知正方形ABCD中,F为对角线BD(不含B点)上任意一点,△ABE为正三角形,若BF=BG且∠FBG=60°,连接EG、AF、CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com