
分析 由于D、E分别是AB、BC的中点,则DE是△ABC的中位线,那么DE=$\frac{1}{2}$AC,同理有EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$BC,于是易求△DEF的周长.
解答 解:如图所示,
∵D、E分别是AB、BC的中点,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$AC,
同理有EF=$\frac{1}{2}$AB,DF=$\frac{1}{2}$BC,
∴△DEF的周长=$\frac{1}{2}$(AC+BC+AB)=$\frac{1}{2}$×12=6cm.
故答案为:6.
点评 本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
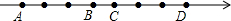 已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )
已知如图:数轴上A,B,C,D四点对应的有理数分别是整数a,b,c,d.且有c-2a=7,则原点应是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
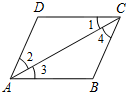 如图所示,下列推理及所注理由错误的是( )
如图所示,下列推理及所注理由错误的是( )| A. | ∵∠1=∠3,∴AB∥CD(内错角相等,两直线平行) | |
| B. | ∵AB∥CD,∴∠1=∠3(两直线平行,内错角相等) | |
| C. | ∵AD∥BC,∴∠2=∠4(两直线平行,内错角相等) | |
| D. | ∵∠2=∠4,∴AB∥CD(内错角相等,两直线平行) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然事件的概率是1 | |
| B. | 如果某种游戏活动的中奖率为40%,那么参加这种活动10次必有4次中奖 | |
| C. | 了解一批灯泡的使用寿命适合用抽样调查 | |
| D. | 数据1、2、2、3的平均数是2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
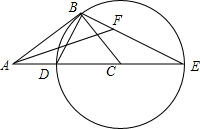 如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com