
 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边. 分析 易得当R在PN上运动时,面积不断在增大,当到达点P时,面积开始不变,到达Q后面积不断减小,得到PN和QP的长度,根据当R在PQ上运动时,△MNR的面积不变且面积最大,面积为$5×4×\frac{1}{2}$=10,当y=9时,9<10,即可解答.
解答 解:∵x=4时,及R从N到达点P时,面积开始不变,
∴PN=4,
同理可得QP=5,
∴MN=PQ=5,PN=QM=4,
当R在PQ上运动时,△MNR的面积不变且面积最大,面积为$5×4×\frac{1}{2}$=10,
当y=9时,9<10,
∴点R在PN边或QM边.
点评 考查动点问题的函数的有关计算;根据所给图形得到矩形的边长是解决本题的关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高(cm) | 170 | 172 | 175 | 178 | 180 | 182 | 185 |
| 人数(个) | 2 | 4 | 5 | 2 | 4 | 3 | 1 |
| A. | 185,178 | B. | 178,175 | C. | 175,178 | D. | 175,175 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 8 |
| 第2组 | 60≤x<70 | 16 |
| 第3组 | 70≤x<80 | a |
| 第4组 | 80≤x<90 | 32 |
| 第5组 | 90≤x<100 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
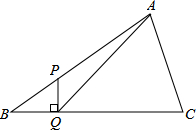 如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.
如图,在△ABC中,∠B=30°,点P是AB上一点,AP=3BP,PQ⊥BC于Q,连接AQ,则cos∠AQC的值为$\frac{3\sqrt{129}}{43}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:
如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com