
【题目】顺次联结对角线互相垂直的等腰梯形各边中点所得的四边形是( )
A. 平行四边形B. 矩形C. 菱形D. 正方形
科目:初中数学 来源: 题型:
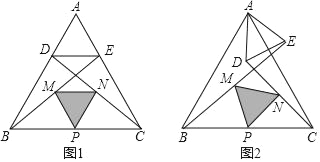
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
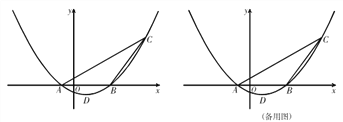
【题目】如图 ,在平面直角坐标系中 ,已知二次函数y=ax2+bx+c (a≠0)
的图象经过 A(-1,0),B(3,0),C(6,4)三点.
(1)求此二次函数解析式和顶点 D 的坐标;
(2)①E为抛物线对称轴上一点,过点E作FG//x 轴,分别交抛物线于F、G两点 ,若![]() ,求点E的坐标;
,求点E的坐标;
② 若抛物线对称轴上点 H 到直线 BC 的距离等于点 H 到 x 轴的距离,则求出点 H
的坐标;
(3)在(2)的条件下,以点I(1,![]() )为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值
)为圆心,IH 的长为半径作⊙I,J 为⊙I上的动点,求是否存在一个定值![]() ,使得 CJ+
,使得 CJ+![]() EJ 的最小值是
EJ 的最小值是![]() 若不存在,请说明理由.若存在,请求出
若不存在,请说明理由.若存在,请求出![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把 6个相同的小正方体摆成如图的几何体.
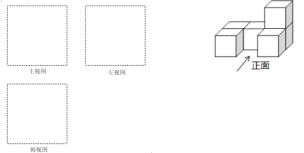
(1)画出该几何体的主视图、左视图、俯视图;
(2)如果每个小正方体棱长为![]() ,则该几何体的表面积是
,则该几何体的表面积是 ![]() .
.
(3)如果在这个几何体上再添加一些相同的小正方体,并并保持左视图和俯视图不变,那么最多可以再 添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们知道图形是由点、线、面组成,结合具体实例,已经感受到“点动成线,线动成面”的现象,下面我们一起来进一步探究:
(概念认识)
已知点P和图形M,点B是图形M上任意一点,我们把线段PB长度的最小值叫做点P与图形M之间的距离.
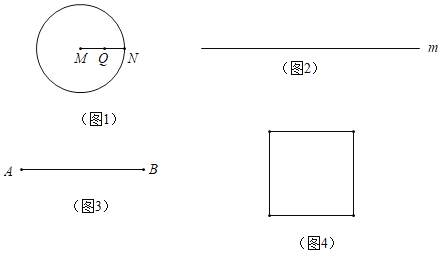
例如,以点M为圆心,1cm为半径画圆如图1,那么点M到该圆的距离等于1cm;若点N是圆上一点,那么点N到该圆的距离等于0cm;连接MN,若点Q为线段MN中点,那么点Q到该圆的距离等于0.5cm,反过来,若点P到已知点M的距离等于1cm,那么满足条件的所有点P就构成了以点M为圆心,1cm为半径的圆.
(初步运用)
(1)如图2,若点P到已知直线m的距离等于1cm,请画出满足条件的所有点P.
(深入探究)
(2)如图3,若点P到已知线段的距离等于1cm,请画出满足条件的所有点P.
(3)如图4,若点P到已知正方形的距离等于1cm,请画出满足条件的所有点P.
查看答案和解析>>
科目:初中数学 来源: 题型:
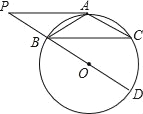
【题目】如图,⊙O中,点A为![]() 中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(Ⅰ)求证:PA是⊙O的切线;
(Ⅱ)若BC=2![]() ,AB=2
,AB=2![]() ,求sin∠ABD的值.
,求sin∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于一点,则有_____________对对顶角,_____________对邻补角.
(2)若3条直线相交于同一点,则有_____________对对顶角,_____________对邻补角.
(3)若4条直线相交于同一点,则有______________对对顶角,__________________对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成___________对对顶角,___________对邻补角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过点
的图象经过点![]() ,交x轴于点A、
,交x轴于点A、![]() 点在B点左侧
点在B点左侧![]() ,顶点为D.
,顶点为D.
![]() 求抛物线的解析式及点A、B的坐标;
求抛物线的解析式及点A、B的坐标;
![]() 将
将![]() 沿直线BC对折,点A的对称点为
沿直线BC对折,点A的对称点为![]() ,试求
,试求![]() 的坐标;
的坐标;
![]() 抛物线的对称轴上是否存在点P,使
抛物线的对称轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
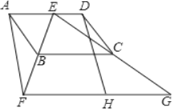
(1)求证:四边形AFHD为平行四边形;
(2)若CB=CE,∠BAE=60°,∠DCE=20°,求∠CBE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com