
分析 (1)原式利用二次根式的乘法法则计算,合并即可得到结果;
(2)原式利用平方差公式及单项式乘以多项式法则计算,去括号合并得到最简结果,把x的值代入计算即可求出值;
(3)方程整理后,利用因式分解法求出解即可.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{3}$=$\sqrt{3}$;
(2)原式=x2-2+x-x2=x-2,
当x=$\sqrt{2}$-4时,原式=$\sqrt{2}$-6;
(3)方程整理得:x2-4x-5=0,即(x-5)(x+1)=0,
解得:x1=5,x2=-1.
点评 此题考查了二次根式的混合运算,整式的混合运算-化简求值,以及解一元二次方程-因式分解法,熟练掌握运算法则是解本题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
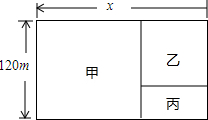 有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)
有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 画图与说理:如图,在△ABC中.
画图与说理:如图,在△ABC中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com