
【题目】如图,△ABC的中线AD、BE、CF相交于点G,H、I分别是BG、CG的中点.
(1)求证:四边形EFHI是平行四边形;
(2)①当AD与BC满足条件 时,四边形EFHI是矩形;
②当AD与BC满足条件 时,四边形EFHI是菱形.
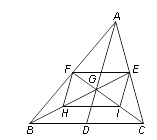
【答案】(1)证明见解析;(2)①AD⊥BC;②2AD=3BC
【解析】试题分析:(1)证出EF、HI分别是△ABC、△BCG的中位线,根据三角形中位线定理可得EF∥BC且EF=![]() BC,HI∥BC且PQ=
BC,HI∥BC且PQ=![]() BC,进而可得EF∥HI且EF=HI.根据一组对边平行且相等的四边形是平行四边形可得结论;
BC,进而可得EF∥HI且EF=HI.根据一组对边平行且相等的四边形是平行四边形可得结论;
(2)①由三角形中位线定理得出FH∥AD,再证出EF⊥FH即可;
②与三角形重心定理得出AG=![]() AD,证出AG=BC,由三角形中位线定理和添加条件得出FH=EF,即可得出结论.
AD,证出AG=BC,由三角形中位线定理和添加条件得出FH=EF,即可得出结论.
试题解析:(1)证明:∵BE,CF是△ABC的中线,∴EF是△ABC的中位线,∴EF∥BC且EF=![]() BC.
BC.
∵H、I分别是BG、CG的中点.,∴HI是△BCG的中位线,∴HI∥BC且HI=![]() BC,∴EF∥HI且EF=HI,∴四边形EFHI是平行四边形.
BC,∴EF∥HI且EF=HI,∴四边形EFHI是平行四边形.
(2)解:①当AD与BC满足条件 AD⊥BC时,四边形EFHI是矩形;理由如下:
同(1)得:FH是△ABG的中位线,∴FH∥AG,FH=![]() AG,∴FH∥AD,∵EF∥BC,AD⊥BC,∴EF⊥FH,∴∠EFH=90°,∵四边形EFHI是平行四边形,∴四边形EFHI是矩形;
AG,∴FH∥AD,∵EF∥BC,AD⊥BC,∴EF⊥FH,∴∠EFH=90°,∵四边形EFHI是平行四边形,∴四边形EFHI是矩形;
故答案为:AD⊥BC;
②当AD与BC满足条件BC=![]() AD时,四边形EFHI是菱形;理由如下:
AD时,四边形EFHI是菱形;理由如下:
∵△ABC的中线AD、BE、CF相交于点G,∴AG=![]() AD,∵BC=
AD,∵BC=![]() AD,∴AG=BC,∵FH=
AD,∴AG=BC,∵FH=![]() AG,EF=
AG,EF=![]() BC,∴FH=EF,又∵四边形EFHI是平行四边形,∴四边形EFHI是菱形;
BC,∴FH=EF,又∵四边形EFHI是平行四边形,∴四边形EFHI是菱形;
故答案为:2AD=3BC.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”,若“关联数”[1,m﹣2]的一次函数是正比例函数,则关于x的方程x2+3x+m=0的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知□ABCD中,直线m绕点A旋转,直线m不经过B、C、D点,过B、C、D分别作BE⊥m于E, CF⊥m于F, DG⊥m于G.
(1)当直线m旋转到如图1位置时,线段BE、CF、DG之间的数量关系是 _;
(2)当直线m旋转到如图2位置时,线段BE、CF、DG之间的数量关系是 _;
(3)当直线m旋转到如图3的位置时,线段BE、CF、DG之间有怎样的数量关系?请直接写出你的猜想,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为多少米?(结果保留整数,测角仪忽略不计, ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com