
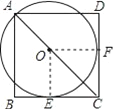
【题目】如图,O为正方形ABCD对角线上一点,以点O为圆心,OA长为半径的
⊙ O与BC相切于点E.
(1)求证:CD是⊙ O的切线;
(2)若正方形ABCD的边长为10,求⊙O的半径.

【答案】(1)见解析;(2)20﹣10![]() .
.
【解析】试题分析:(1)首先连接OE,并过点O作OF⊥CD,由OA长为半径的 O与BC相切于点E,可得OE=OA,OE⊥BC,然后由AC为正方形ABCD的对角线,根据角平分线的性质,可证得OF=OE=OA,即可判定CD是 O的切线;
(2)由正方形ABCD的边长为10,可求得其对角线的长,然后由设OA=r,可得OE=EC=r,由勾股定理求得OC=![]() r,则可得方程r+
r,则可得方程r+![]() r=10
r=10![]() ,继而求得答案.
,继而求得答案.
试题解析:(1)证明:连接OE,并过点O作OF⊥ CD.
∵ BC切⊙ O于点E,
∴OE⊥ BC,OE=OA,
又∵AC为正方形ABCD的对角线,
∴∠ ACB=∠ ACD,
∴OF=OE=OA,
即:CD是⊙ O的切线.
(2)解:∵ 正方形ABCD的边长为10,
∴A B=BC=10,∠ B=90°,∠ ACB=45°,
∴AC=![]() =10
=10![]() ,
,
∵OE⊥ BC,
∴OE=EC,
设OA=r,则OE=EC=r,
∴OC=![]() ,
,
∵OA+OC=AC,
∴r+![]() r=10
r=10![]() ,
,
解得:r=20﹣10![]() .
.
∴⊙O的半径为:20﹣10![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
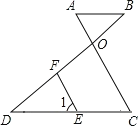
【题目】如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
(1)求证:FE∥OC;
(2)若∠BOC比∠DFE大20,求∠OFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A.中位数就是一组数据中最中间的一个数
B.这组数据0,2,3,3,4,6的方差是2.1
C.一组数据的标准差越大,这组数据就越稳定
D.如果![]() 的平均数是
的平均数是![]() ,那么
,那么![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“甲型H1N1”,某校对教室采用药薰消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的含药量低于1.6mg时,生方可进教室,那么从消毒开始,至少需要几分钟后,生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①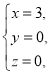 ②
②![]() ③
③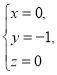 这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组
这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组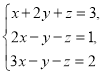 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,求∠A+∠AEC+∠C的度数.
解:过点E作EF∥AB.
∵EF∥AB(已作)
∴∠A+∠AEF=180°(______)
又∵AB∥CD(已知)
∴EF∥CD(______)
∴∠CEF+∠______=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C=360°(等式性质)
即∠A+∠AEC+∠C=______.
(2)根据上述解题及作辅助线的方法,在图2中,AB∥EF,则∠B+∠C+∠D+∠E=______.
(3)根据(1)和(2)的规律,图3中AB∥GF,猜想:∠B+∠C+∠D+∠E+∠F=______.
(4)如图4,AB∥CD,在B,D两点的同一侧有M1,M2,M3,…Mn共n个折点,则∠B+∠M1+∠M2+…+∠Mn+∠D的度数为______(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,P是边AB上的一点,连接CP.
(1)要使△ACP∽△ABC,还需要补充的一个条件是_____.
(2)若△ACP∽△ABC,且AC=![]() ,AB=3,求AP的长.
,AB=3,求AP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com