
分析 设这些蚂蚁应集中到第x个蚂蚁窝(1≤x≤30且x为正整数),根据题意得出100+200+…+3000=46500,100+200+…+100x=50(1+x)x=$\frac{46500}{2}$,解得:x=$\frac{-1±\sqrt{1861}}{2}$,当x=21时,(1+x)x=462,当x=22时,(1+x)x=506,j即可得出结论.
解答 解:设这些蚂蚁应集中到第x个蚂蚁窝(1≤x≤30且x为正整数),
∵100+200+…+3000=100(1+2+…+30)=100×$\frac{31×30}{2}$=46500,
100+200+…+100n=100(1+2+…+x)=100×$\frac{(1+x)x}{2}$=50(1+x)x=$\frac{46500}{2}$,
整理得:(1+x)x=465,
解得:x=$\frac{-1±\sqrt{1861}}{2}$,
当x=21时,(1+x)x=462;当x=22时,(1+x)x=506,
∴这些蚂蚁应集中到第 21个蚂蚁窝;
故答案为:21.
点评 本题考查了数字的变化美、最短路径问题、数的计算技巧、一元二次方程的解法;根据题意得出方程是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 抽取柑橘总质量n千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| 损坏柑橘质量m千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.94 |
| 柑橘损坏频率m/n | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
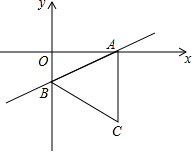 如图,直线y=(m+1)x+2(m-1)(m为常数)与x轴交于点A,与y轴交于点B,△ABC是等边三角形(其中A,B,C为逆时针标注的三个点)
如图,直线y=(m+1)x+2(m-1)(m为常数)与x轴交于点A,与y轴交于点B,△ABC是等边三角形(其中A,B,C为逆时针标注的三个点)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 顶角相等的两个等腰三角形 | |
| B. | 两个等边三角形 | |
| C. | 各有一个角是45°,腰长都是3cm的两个等腰三角形 | |
| D. | 底边和顶角都相等的两个等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com