
【题目】如图,已知点P是△ABC两边中垂线的交点,若∠A=72°,则∠BPC=____.

【答案】144°
【解析】
连接AP并延长交BC于D,由垂直平分线上的点到线段两端的距离相等,可得PA=PB=PC,再由三角形外角的性质求得∠BPC=2∠BAC,即可得出答案.
如图所示,连接AP并延长交BC于D,

∵点P在BC的中垂线上
∴PB=PC
同理可得PB=PA
∴PA=PB=PC
∴∠PAB=∠PBA,∠PAC=∠PCA
又∵∠BPD=∠PAB+∠PBA,∠CPD=∠PAC+∠PCA
∴∠BPD=2∠PAB,∠CPD=2∠PAC
∴∠BPC=∠BPD+∠CPD=2∠PAB+2∠PAC=2(∠PAB+∠PAC)=2∠BAC
∵∠A=72°,
∴∠BPC=2∠A=144°
故答案为:144°.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB和△APQ都是等边三角形.
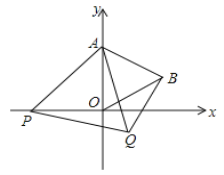

⑴求点B的坐标;
⑵试判断直线AB与直线BQ的位置关系,并证明;
⑶连接OQ,当OQ∥AB时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生2018年初中毕业体育考试的成绩统计如表
成绩(分) | 85 | 89 | 92 | 94 | 95 | 98 | 99 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 6 | 7 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次考试成绩的众数是95分
C. 该班学生这次考试成绩的中位数是95分
D. 该班学生这次考试成绩的平均数是95
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 中,AB=AD,点B关于AC的对称点B′恰好落在CD上,若∠BAD=![]() ,则∠ACB的度数为( )
,则∠ACB的度数为( )

A. ![]() α B. 90°-
α B. 90°-![]() α C. 45° D. α-45°
α C. 45° D. α-45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com