
阅读材料:
如下图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:![]() ,即三角形面积等于水平宽与铅垂高乘积的一半.
,即三角形面积等于水平宽与铅垂高乘积的一半.
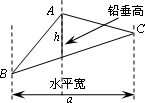
解答下列问题:
如下图,抛物线顶点坐标为点C(1,4),交x轴于点A(3,0),交y轴于点B.
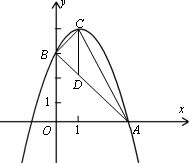
(1)求抛物线和直线AB的解析式;
(2)点P是抛物线(在第一象限内)上的一个动点,连结PA,PB,当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB;
(3)是否存在一点P,使S△PAB=![]() S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
S△CAB,若存在,求出P点的坐标;若不存在,请说明理由.
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
科目:初中数学 来源: 题型:044
.阅读材料:
如图在四边形ABCD中,对角线AC⊥BD,垂足为P.
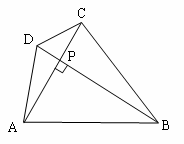
求证:S四边形ABCD=![]()
证明:AC⊥BD→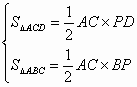
∴S
四边形ABCD=S△ACD+S△ACB==
解答问题:
(1
)上述证明得到的性质可叙述为___________________________.(2
)已知:如下图,等腰梯形ABCD中,AD∥BC,对角线AC⊥BD且相交于点P,BD=10cm,利用上述的性质求梯形的面积.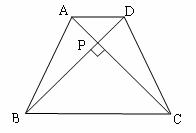
查看答案和解析>>
科目:初中数学 来源:宁夏自治区月考题 题型:解答题
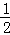 ah,即三角形面积等于水平宽与铅垂高乘积的一半。
ah,即三角形面积等于水平宽与铅垂高乘积的一半。 S△CAB?若存在,求出P点的坐标;若不存在,请说明理由。
S△CAB?若存在,求出P点的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源:专项题 题型:解答题
 AC·BD。
AC·BD。
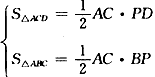
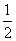 AC·PD+
AC·PD+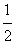 AC·BP=
AC·BP=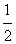 AC·(PD+PB)=
AC·(PD+PB)=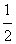 AC·BD。
AC·BD。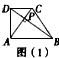

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com