
【题目】甲、乙两车从A地出发,沿同一路线驶向B地. 甲车先出发匀速驶向B地,40 min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时. 由于满载货物,为了行驶安全,速度减少了50 km/h,结果与甲车同时到达B地. 甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60 km/h;③乙出发80 min追上甲;④乙刚到达货站时,甲距B地180 km.其中正确的有( )
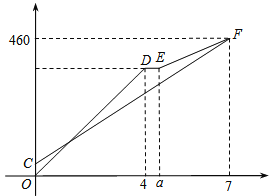
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
由线段![]() 所代表的意思,结合装货半小时,可得出
所代表的意思,结合装货半小时,可得出![]() 的值,从而判断出①成立;
的值,从而判断出①成立;
结合路程=速度×时间,能得出甲车的速度,从而判断出②成立;
设出乙车刚出发时的速度为![]() 千米/时,则装满货后的速度为
千米/时,则装满货后的速度为![]() 千米/时,由路程=速度×时间列出关于
千米/时,由路程=速度×时间列出关于![]() 的一元一次方程,解出方程即可得知乙车的初始速度,由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间,从而得出③成立;
的一元一次方程,解出方程即可得知乙车的初始速度,由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间,从而得出③成立;
由乙车刚到达货站的时间,可以得出甲车行驶的总路程,结合![]() 、
、![]() 两地的距离即可判断④也成立.
两地的距离即可判断④也成立.
综上可知①②③④皆成立.
![]() 线段
线段![]() 代表乙车在途中的货站装货耗时半小时,
代表乙车在途中的货站装货耗时半小时,
![]()
![]() (小时),即①成立;
(小时),即①成立;
![]() 分钟
分钟![]() 小时,
小时,
甲车的速度为![]() (千米/时),即②成立;
(千米/时),即②成立;
设乙车刚出发时的速度为![]() 千米/时,则装满货后的速度为
千米/时,则装满货后的速度为![]() 千米/时,
千米/时,
根据题意可知:![]() ,
,
解得:![]() ,
,
乙车发车时,甲车行驶的路程为![]() (千米),
(千米),
乙车追上甲车的时间为![]() (小时),
(小时),
![]() 小时
小时![]() 分钟,即③成立;
分钟,即③成立;
乙车刚到达货站时,甲车行驶的时间为![]() 小时,
小时,
此时甲车离![]() 地的距离为
地的距离为![]() (千米),即④成立;
(千米),即④成立;
综上可知正确的有:①②③④.
故选:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).

A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成语“运筹帷幄”中“筹”的原意是指《孙子算经》中记载的“算筹”.算筹是中国古代用来进行计算的工具,它是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵、横两种形式(如图).
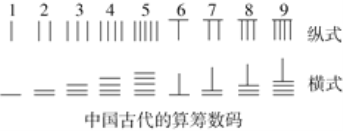
当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的算筹需要纵、横相间:个位,百位,万位数用纵式表示;十位,千位,十万位数用横式表示:“0”用空位来代替,以此类推,如:数3306用算筹表示成![]() .用算筹
.用算筹![]() 表示的数是______.
表示的数是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气魄雄伟的大礼堂座落在渝中区学田湾,它是一座仿古民族建筑.“五一”期间,小明和妈妈到重庆大礼堂参观游玩.参观结束后,穿过人民广场到达A处,回望礼堂,更显气势雄伟,金碧辉煌.此时,在A点观察到礼堂顶端的仰角为30°,沿着坡度为1:3的斜坡AB走一段距离到达B点,观察到礼堂顶端 的仰角是22°,测得点A与BC之间的水平距离![]() 米,则大礼堂的高度DE为( )米.(精确到1米.参考数据:
米,则大礼堂的高度DE为( )米.(精确到1米.参考数据: ![]() ,
, ![]() .)
.)
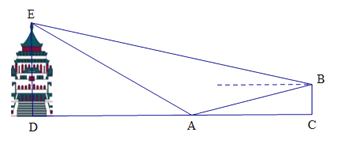
A. 58 B. 60 C. 62 D. 64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰直角三角形ABC中,∠BAC=90°,AB=AC,D是斜边BC的中点,连接AD.
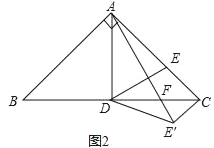
(1)如图1,E是AC的中点,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′,当AD=![]() 时,求AE的值.
时,求AE的值.
(2)如图2,在AC上取一点E,使得CE=![]() AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
AC,连接DE,将△CDE沿CD翻折到△CDE′,连接AE′交BC于点F,求证:DF=CF.
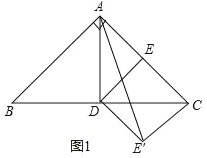
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合),通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于点E,延长EG 交CD于点F.如图①,当点H与点C重合时,易证得FG=FD(不要求证明);如图②,当点H为边CD上任意一点时,求证:FG=FD.
【应用】在图②中,已知AB=5,BE=3,则FD= ,△EFC的面积为 .(直接写结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们给出如下定义:数轴上给定两点![]() ,
,![]() 以及一条线段
以及一条线段![]() ,若线段
,若线段![]() 的中点
的中点![]() 在线段
在线段![]() 上(点
上(点![]() 可以与点
可以与点![]() 或
或![]() 重合),则称点
重合),则称点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称.下图为点
径向对称.下图为点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称的示意图.
径向对称的示意图.

解答下列问题:
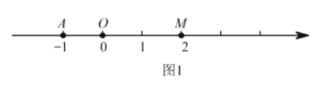
如图1,在数轴上,点![]() 为原点,点
为原点,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
(1)①点![]() ,
,![]() ,
,![]() 分别表示的数为-3,
分别表示的数为-3,![]() ,3,在
,3,在![]() ,
,![]() ,
,![]() 三点中, 与点
三点中, 与点![]() 关于线段
关于线段![]() 径向对称;
径向对称;
②点![]() 表示的数为
表示的数为![]() ,若点
,若点![]() 与点
与点![]() 关于线段
关于线段![]() 径向对称,则
径向对称,则![]() 的取值范围是 ;
的取值范围是 ;
(2)在数轴上,点![]() ,
,![]() ,
,![]() 表示的数分别是-5,-4,-3,当点
表示的数分别是-5,-4,-3,当点![]() 以每秒1个单位长度的速度向正半轴方向移动时,线段
以每秒1个单位长度的速度向正半轴方向移动时,线段![]() 同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为
同时以每秒3个单位长度的速度向正半轴方向移动.设移动的时间为![]() (
(![]() )秒,问
)秒,问![]() 为何值时,线段
为何值时,线段![]() 上至少存在一点与点
上至少存在一点与点![]() 关于线段
关于线段![]() 径向对称.
径向对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲船逆水,静水速度为28海里/时;乙船顺水,静水速度为12海里/时,两船相距60海里.已知水流速度为3海里/时,两船同时相向而行.
(1)两船同时航行1小时,求此时两船之间的距离;
(2)再(1)的情况下,两船再继续航行1小时,求此时两船之间的距离;
(3)求两船从开始航行到两船相距12海里,需要多长时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com