
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,﹣3),并且以x=1为对称轴.
(1)求此函数的解析式;
(2)作出二次函数的大致图象;
(3)在对称轴x=1上是否存在一点P,使△PAB中PA=PB?若存在,求出P点的坐标;若不存在,说明理由.
【答案】(1)解析式为y=x2﹣2x﹣3;(2)画图见解析;(3)存在,点P的坐标为(1,﹣1).
【解析】试题分析:(1)根据对称轴的公式x=![]() 和函数的解析式,将
和函数的解析式,将![]() =1和A(3,0),B(2,﹣3)代入函数解析式,组成方程组解答即可;
=1和A(3,0),B(2,﹣3)代入函数解析式,组成方程组解答即可;
(2)求出图象与坐标轴的交点坐标,描点即可;
(3)根据两点之间距离公式解答即可.
试题解析:解:(1)根据题意得:  ,解得:
,解得: 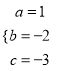 ,∴解析式为y=x2﹣2x﹣3;
,∴解析式为y=x2﹣2x﹣3;
(2)二次函数图象如图:
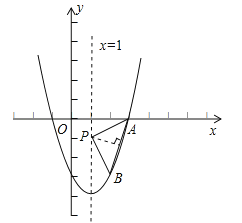
(3)存在.作AB的垂直平分线交对称轴x=1于点P,连接PA、PB,则PA=PB,设P点坐标为(1,m).∵PA=PB,∴22+m2=(﹣3﹣m)2+1,解得:m=﹣1,∴点P的坐标为(1,﹣1).


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
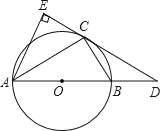
【题目】如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=![]() ,求BD和BC的长.
,求BD和BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,高AD和BE交于点H,且∠1=∠2=22.5°,下列结论:①∠1=∠3;②BD+DH=AB;③2AH=BH;④若CD=![]() ,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.
,则BH=3;⑤若DF⊥BE于点F,则AE-FH=DF;正确的有( )个.

A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b在数轴上的位置如图所示,且|a|<|b|,下列各式中正确的个数是( )
①a+b<0;②b﹣a>0;③![]() ;④3a﹣b>0;⑤﹣a﹣b>0.
;④3a﹣b>0;⑤﹣a﹣b>0.
![]()
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com