
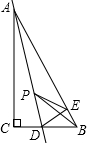
 如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$.
如图,在Rt△ABC中,∠C=90°,∠ABC=60°,点D是BC边上的点,CD=$\sqrt{3}$,将△ACD沿直线AD折叠,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是3+$\sqrt{3}$. 分析 连接CE,交AD于M,根据折叠和等腰三角形性质得出当P和D重合时,PE+BP的值最小,即可此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,先求出BC和BE长,代入求出即可.
解答 解:如图,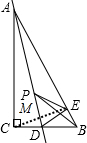
连接CE,交AD于M,
∵沿AD折叠C和E重合,
∴∠ACD=∠AED=90°,AC=AE,∠CAD=∠EAD,
∴AD垂直平分CE,即C和E关于AD对称,CD=DE=$\sqrt{3}$,
∴当P和D重合时,PE+BP的值最小,即此时△BPE的周长最小,最小值是BE+PE+PB=BE+CD+DB=BC+BE,
∵∠DEA=90°,
∴∠DEB=90°,
∵∠BAC=30°,
∴∠B=60°,
∵DE=$\sqrt{3}$,
∴BE=1,BD=2,
即BC=2+$\sqrt{3}$,
∴△PEB的周长的最小值是BC+BE=2+$\sqrt{3}$+1=3+$\sqrt{3}$.
故答案为:3+$\sqrt{3}$.
点评 本题考查了折叠性质,等腰三角形性质,轴对称-最短路线问题,勾股定理,含30度角的直角三角形性质的应用,关键是求出P点的位置.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 1 | C. | -1或8 | D. | -1或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
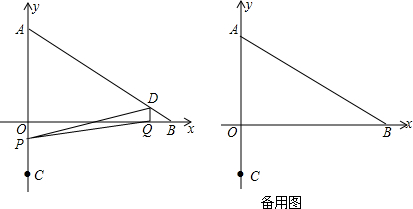
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
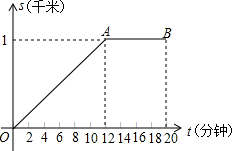 小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.
小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com