
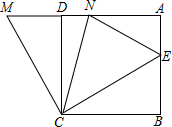
 如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CM.
如图,在正方形ABCD中,E是AB上一点,M是AD延长线上一点,且MD=BE,连接CM.分析 (1)根据正方形的性质得到CD=BC,∠ADC=∠B=90°,
根据全等三角形的性质得到∠BCE=∠DCM;
(2)根据全等三角形的性质得到∠BCE=∠DCM,CE=CM,根据全等三角形的性质得到NE=MN,等量代换即可得到结论;
(3)设正方形的边长为x根据勾股定理即可得到结论.
解答 (1)证明:在正方形ABCD中,
∵CD=BC,∠ADC=∠B=90°,
∴∠MDC=∠B=90°,
在△BCE与△CDM中,$\left\{\begin{array}{l}{BC=CD}\\{∠B=∠CDM}\\{BE=DM}\end{array}\right.$,
∴△BCE≌△CDM,
∴∠BCE=∠DCM;
(2)∵∠NCE=45°,
∴∠BCE+∠DCN=45°,
∵△BCE≌△CDM,
∴∠BCE=∠DCM,CE=CM,
在△CEN与△CMN中,$\left\{\begin{array}{l}{CM=CE}\\{∠ECN=∠MCN}\\{CN=CN}\end{array}\right.$,
∴△CEN≌△CMN,
∴NE=MN,
∵MN=MD+DN=BE+DN,
∴NE=BE+DN;
(3)设正方形的边长为x,
∵NE=BE+DN=MD+DN=3+2=5,AN=AD-DN=x-2,AE=x-3,
∵NE2=AN2+AE2,
∴52=(x-2)2+(x-3)2,
解得:x=6,或x=-1(不合题意,舍去),
∴正方形的边长是6.
点评 本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,熟练掌握全等三角形的判定和性质是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
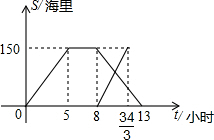 钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往钓鱼岛A海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往钓鱼岛.如图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
钓鱼岛是我国渤海海峡上的一颗明珠,渔产丰富.一天某渔船离开港口前往钓鱼岛A海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向钓鱼岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往钓鱼岛.如图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
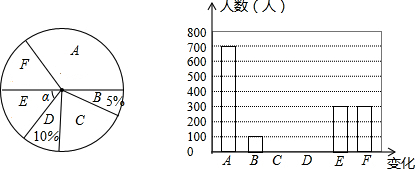
 某学校为了推动运动普及,拟成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:
某学校为了推动运动普及,拟成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种类 | A选项 | B选项 | C选项 | D选项 | E选项 | F选项 |
| 实施“二孩”的可能变化 | 延缓社会老龄化 | 家庭发展能力提升 | 导致人口暴增 | 增加公共资源压力 | 出生人口性别趋衡 | 劳动年龄人口增加 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com