
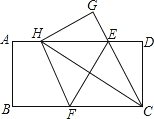
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;
②EC平分∠DCH;
③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2![]() .
.
以上结论中,你认为正确的有( )个.
A.1 B.2 C.3 D.4
【答案】C.
【解析】
试题分析:先判断出四边形CFHE是平行四边形,再根据翻折的性质可得CF=FH,然后根据邻边相等的平行四边形是菱形证明,判断出①正确;
根据菱形的对角线平分一组对角线可得∠BCH=∠ECH,然后求出只有∠DCE=30°时EC平分∠DCH,判断出②错误;
点H与点A重合时,设BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,点G与点D重合时,CF=CD,求出BF=4,然后写出BF的取值范围,判断出③正确;
过点F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判断出④正确.
试题解析:∵FH与CG,EH与CF都是矩形ABCD的对边AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四边形CFHE是平行四边形,
由翻折的性质得,CF=FH,
∴四边形CFHE是菱形,(故①正确);
∴∠BCH=∠ECH,
∴只有∠DCE=30°时EC平分∠DCH,(故②错误);
点H与点A重合时,设BF=x,则AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8-x)2,
解得x=3,
点G与点D重合时,CF=CD=4,
∴BF=4,
∴线段BF的取值范围为3≤BF≤4,(故③正确);
过点F作FM⊥AD于M,
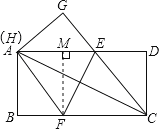
则ME=(8-3)-3=2,
由勾股定理得,
EF=![]() ,(故④正确);
,(故④正确);
综上所述,结论正确的有①③④共3个.
故选C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】 (2016山东威海第21题)一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用着六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A(2,3)向左平移2个单位长度得到点A′,点A′关于x轴的对称点是A″,则点A″的坐标为( )
A. (0,-3) B. (4,-3) C. (4,3) D. (0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王鹏家里购买了一套小户型商品房,准备将地面铺上相同的地砖,地面结构如下图,根据图中的数据(单位:m),解答下列问题. 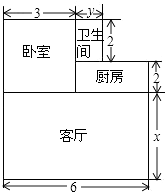
(1)用含x,y的代数式表示地面总面积;
(2)已知铺1m2地砖的平均费用为210元,当x=5,y=1时,求铺这套商品房所需地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点. 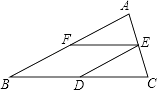
(1)求证:四边形BDEF是菱形;
(2)若AB=12cm,求菱形BDEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 ![]() 的图象分别与x轴、y轴交于A、B,以线段AB为边在第一象限内作等腰Rt△ABC,使∠BAC=90°.
的图象分别与x轴、y轴交于A、B,以线段AB为边在第一象限内作等腰Rt△ABC,使∠BAC=90°. 
(1)分别求点A、C的坐标;
(2)在x轴上求一点P,使它到B、C两点的距离之和最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
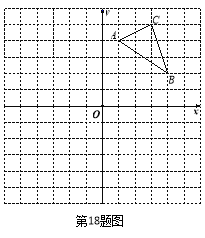
【题目】(辽宁丹东)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com