练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

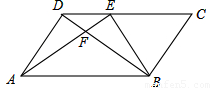
    如图，在▱ABCD中，E为CD上一点，DE：CE=2：3，连接AE、BE、BD，且AE、BD交于点F，则S△DEF：S△EBF：S△ABF=______________.

     

     

    【答案】

    4：10：25.

    【解析】

    试题分析：相似三角形的面积比等于相似比的平方，同高的三角形的面积之比等于底的比．根据已知可得到相似三角形：△DFE∽△BFA，从而可得到其相似比：DE：AB=2：5，DF：FB=2：5，再根据相似三角形的面积比等于相似比的平方可得到：S△DEF：S△EBF：S△ABF=4：10：25．故填：4：10：25．

    考点：1、相似三角形的判定与性质；2、平行四边形的性质．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2013-2014学年山东泰安高新区第一中学九年级第一学期期末模拟数学试卷（解析版） 题型：选择题

    如图，在▱ABCD中，AC与BD相交于点O，则下列结论不一定成立的是（　　）

    A．BO=DO    B．CD=AB    C．∠BAD=∠BCD    D．AC=BD

     

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（湖南湘西卷）数学（解析版） 题型：选择题

    如图，在▱ABCD中，E是AD边上的中点，连接BE，并延长BE交CD延长线于点F，则△EDF与△BCF的周长之比是【    】

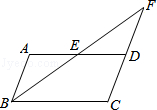
    A．1：2       B．1：3       C．1：4       D．1：5

     

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（四川雅安卷）数学（解析版） 题型：填空题

    如图，在▱ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF=　    　..

     

     

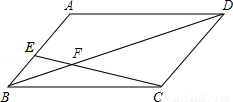
    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（吉林长春卷）数学（解析版） 题型：解答题

    如图①，在▱ABCD中，AB=13，BC=50，BC边上的高为12．点P从点B出发，沿B﹣A﹣D﹣A运动，沿B﹣A运动时的速度为每秒13个单位长度，沿A﹣D﹣A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度．P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．

    （1）当点P沿A﹣D﹣A运动时，求AP的长（用含t的代数式表示）．

    （2）连结AQ，在点P沿B﹣A﹣D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式．

    （3）过点Q作QR∥AB，交AD于点R，连结BR，如图②．在点P沿B﹣A﹣D运动过程中，当线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值．

    （4）设点C、D关于直线PQ的对称点分别为C′、D′，直接写出C′D′∥BC时t的值．

     

    查看答案和解析>>

    科目：初中数学 来源：2011年全国八年级第一学期期中考试数学卷 题型：填空题

    如图，在▱ABCD中，点 E、F在对角线AC上，要使图中能够出现三对全等三角形，只需添加一个条件                   。（填写一种即可）

     

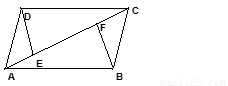
    查看答案和解析>>

    同步练习册答案