
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是
| A.5个 | B.4个 | C.3个 | D.2个 |
B
解析分析:∵二次函数y=ax2+bx+c(a≠0)过点(0,1)和(﹣1,0),∴c=1,a﹣b+c=0。
①∵抛物线的对称轴在y轴右侧,∴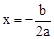 x>0。∴a与b异号。∴ab<0,正确。
x>0。∴a与b异号。∴ab<0,正确。
②∵抛物线与x轴有两个不同的交点,∴b2﹣4ac>0。
∵c=1,∴b2﹣4a>0,即b2>4a。正确。
④∵抛物线开口向下,∴a<0。
∵ab<0,∴b>0。
∵a﹣b+c=0,c=1,∴a=b﹣1。∴b﹣1<0,即b<1。∴0<b<1,正确。
③∵a﹣b+c=0,∴a+c=b。∴a+b+c=2b>0。
∵b<1,c=1,a<0,∴a+b+c=a+b+1<a+1+1=a+2<0+2=2。∴0<a+b+c<2,正确。
⑤抛物线y=ax2+bx+c与x轴的一个交点为(﹣1,0),设另一个交点为(x0,0),则x0>0,
由图可知,当﹣1<x<x0时,y>0;当x>x0时,y<0。
∴当x>﹣1时,y>0的结论错误。
综上所述,正确的结论有①②③④。故选B。


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:单选题
抛物线y=ax2+bx+c(a<0)如图所示,则关于x的不等式ax2+bx+c>0的解集是
| A.x<2 | B.x>﹣3 | C.﹣3<x<1 | D.x<﹣3或x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1,它与x轴交点为O、A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( ).
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
(2013年浙江义乌3分)如图,抛物线y=ax2+bx+c与x轴交于点A(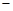 1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:
①当x>3时,y<0;②3a+b>0;③ ;④3≤n≤4中,
;④3≤n≤4中,
正确的是【 】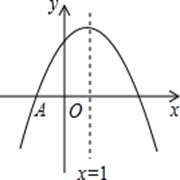
| A.①② | B.③④ | C.①④ | D.①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
点A(2,y1)、B(3,y2)是二次函数y=x2-2x+1的图象上两点,则y1与y2的大小关系为y1________y2(填“>”、“<”、“=”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com