
【题目】下列计算正确的是( )
A. a2·a3=a6 B. (-2ab)2=4a2b2 C. (a2)3=a5 D. a6÷a3=a2
科目:初中数学 来源: 题型:
【题目】46中8年级11班为开展“迎2013年新春”的主题班会活动,派了小林和小明两位同学去学校附近的超市购买钢笔作为奖品,已知该超市的英雄牌钢笔每支8元,派克牌钢笔每支4.8元,他们要购买这两种笔共40支.
(1)如果他们两人一共带了240元,全部用于购买奖品,那么能买这两种笔各多少支?
(2)小林和小明根据主题班会活动的设奖情况,决定所购买的英雄牌钢笔数量要少于派克牌钢笔的数量的![]() ,但又不少于派克牌钢笔的数量的
,但又不少于派克牌钢笔的数量的![]() 。如果他们买了英雄牌钢笔
。如果他们买了英雄牌钢笔![]() 支,买这两种笔共花了
支,买这两种笔共花了![]() 元,
元,
①请写出![]() (元)关于
(元)关于![]() (支)的函数关系式,并求出自变量
(支)的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
②请帮他们计算一下,这两种笔各购买多少支时,所花的钱最少,此时花了多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].

(1)、如图①,对△ABC作变换[50°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)
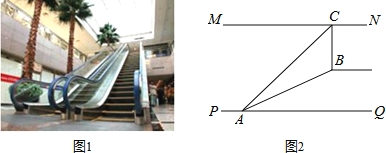
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合单价和的一半定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
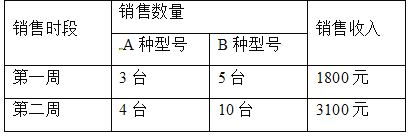
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com