
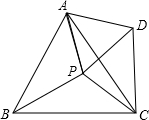
 如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9.
如图,P是等边三角形ABC内一点,∠APB、∠BPC、∠CPA的度数比为4:5:6,以AP为边作正△APD,连接DC,则△PDC的三个内角度数从小到大的比为3:5:9. 分析 可先求出∠APB、∠BPC、∠CPA的度数,就能求出∠DPC的度数,然后证明△APB和△ADC全等,从而证出∠APB=∠ADC,继而求出∠PDC的度数,从而能求出三个角的度数并能求出比值.
解答 解:∵∠APB、∠BPC、∠CPA的度数比为4:5:6,
∴∠APB=360°×$\frac{4}{15}$=96°,
∠BPC=360°×$\frac{5}{15}$=120°,
∠CPA=360°×$\frac{7}{15}$=168°,
∴∠DPC=168°-60°=108°,
在△APB和△ADC中$\left\{\begin{array}{l}{AB=AC}\\{∠BAP=∠CAD}\\{AP=AD}\end{array}\right.$,
∴△APB≌△ADC,
∴∠APB=∠ADC=96°,
∴∠PDC=96°-60°=36°,
∴∠PCD=180°-36°-108°=36°,
36:60:108=3:5:9.
故答案为:3:5:9
点评 本题考查周角的概念,等边三角形的三条边相等三个角为60°以及全等三角形的判定和性质.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
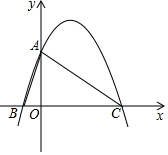 如图,△ABC是直角三角形,∠BAC=90°,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,如图所示建立平面直角坐标系.
如图,△ABC是直角三角形,∠BAC=90°,AB=2$\sqrt{5}$,AC=4$\sqrt{5}$,如图所示建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
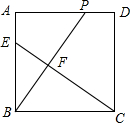 如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.
如图所示,正方形ABCD中,AB=1,点E从点B出发到点A做匀速运动,点P从点D开始到点A做匀速运动,且BP⊥CE,垂足为点F,连接PE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
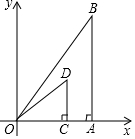 如图,在平面直角坐标系中,△OBA∽△DOC,点A、C都在x轴的正半轴上,点B的坐标为(6,8),∠BAO=∠OCD=90°,OD=5.
如图,在平面直角坐标系中,△OBA∽△DOC,点A、C都在x轴的正半轴上,点B的坐标为(6,8),∠BAO=∠OCD=90°,OD=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com