
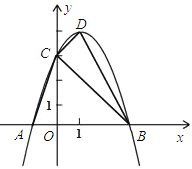
【题目】如图,已知抛物线y=- x2+bx+c与x轴交于点A(-1,0)和B,与y轴交于点C(0,3).
(1)求此抛物线的解析式及点B的坐标;
(2)设抛物线的顶点为D,连接CD、DB、CB、AC.
①求证:△AOC∽△DCB;②在坐标轴上是否存在与原点O不重合的点P,使以P、A、C为顶点的三角形与△DCB相似?若存在,请直接写出点P的坐标;若不存在,请说明理由;
【答案】(1)(3,0);(2)①见解析, ② P1(9,0)或P2(0, ![]() )
)
【解析】试题分析:(1)由C(0,3)得出抛物线解析式为y=-x2+bx+3,将点A的横纵坐标代入解析式求出b,令y=0,解出x即可得点B 的坐标;(2)作DE⊥y轴交于点E,不难求出∠ACB=∠DCE=45°, 则∠DCB=∠AOC=90°,由勾股定理求出CD、BC=的长度,不难发现![]() ,即可证明△AOC∽△DCB;②分情况讨论:1.以C为顶点的角是90°时;2.以A为顶点的角是90°时,分别求出点P的坐标即可.
,即可证明△AOC∽△DCB;②分情况讨论:1.以C为顶点的角是90°时;2.以A为顶点的角是90°时,分别求出点P的坐标即可.
试题解析:
解:(1)∵C(0,3),∴抛物线解析式为y=-x2+bx+3,
∵A(-1,0),∴-1-b+3=0,解得b=2.
∴抛物线的解析式为:y=-x2+2x+3,
令y=0,则-x2+2x+3=0,解得:x1=-1,x2=3,
∴点B的坐标是(3,0);
(2)①证明:作DE⊥y轴交于点E,
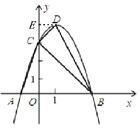
可求得顶点D(1,4),OA=1,OC=OB=3,
∴∠OCB=45°,DE=1,EO=4,
∴EC=1,
∴∠DCE=45°,
故∠DCB=90°=∠AOC,
由勾股定理求得:CD=![]() ,BC=3
,BC=3![]() ,
,
∴![]() ,
,
∴△AOC∽△DCB.
②存在符合条件的点P有两个:P1(9,0)或P2(0, ![]() ).
).
1.以C为顶点的角是90°时,
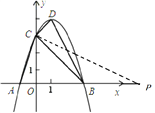
∵∠ACO+∠CAO=90°,∠CPO+∠OCP=90°,
∴∠CPO=∠ACO,
∴∠CPO=∠DBC,
∵∠DCB=∠ACP=90°,
∴△PCA∽△BCD,
∴∠DBC=∠APC,
∴tan∠DBC=tan∠APC,即![]() =
=![]() ,
,
∴OP=9,
∴P(9,0);
2.以A为顶点的角是90°时,
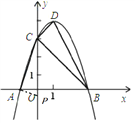
同理可证△AOP∽△BCD,
∴∠DBC=∠PAO,
∴tan∠DBC=tan∠PAO,即![]() =
=![]() ,
,
∴OP=![]() ,
,
∴P(0, ![]() ).
).
综上可得:存在符合条件的点P有两个:P1(9,0)或P2(0, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E, DF∥AB交BC于点F .
(1)求证:四边形BEDF是菱形
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为66万元;本周已售出2辆A型车和1辆B型车,销售额为42万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不超过84万元.问最多可以购买多少辆B型号的新能源汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( )
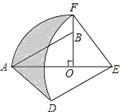
A. π B. ![]() C. 3+π D. 8﹣π
C. 3+π D. 8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来国内生产总值年增长率的变化情况如图所示,从图上看,下列结论中不正确的是( )
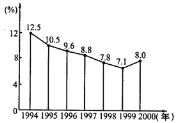
A. 1995—1999年国内生产总值的年增长率逐年减小
B. 2000年国内生产总值的年增长率开始回升
C. 这7年中每年的国内生产总值不断增长
D. 这7年中每年国内生产总值有增有减
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
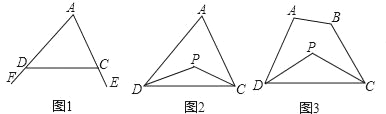
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现:若每箱以50元的价格出售,平均每天销售80箱,价格每提高1元,平均每天少销售2箱.
⑴.求平均每天销售量![]() (箱)与销售价
(箱)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑵.求该批发商平均每天的销售利润![]() (元)与销售价
(元)与销售价![]() (元/箱)之间的函数关系式;
(元/箱)之间的函数关系式;
⑶.当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com