
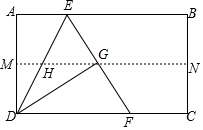
 如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论:分析 ①由折叠的性质和梯形的性质得出①相切;
②周长△ABG为等边三角形,得出②正确;
③由三角函数求出AE,得出③不正确;
④证出∠EBF=∠BEG=∠BFE=60°,得出④正确;即可得出答案.
解答 解:①如图,连接AG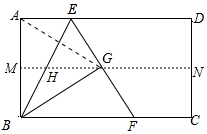
∵MN垂直平分AB,
∴AD∥BC∥MN,
∴AG=BG,EG=FG,①正确,
②根据折叠的性质,可得
AB=BG,
∴AG=AB=BG.
∴△ABG为等边三角形.
∴∠ABG=60°,∠EDG=60°÷2=30°,
即结论②正确;
③∵∠ABG=60°,∠ABE=∠GBE,
∴∠ABE=∠GBE=60°÷2=30°,
∴AE=AB•tan30°=2×$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
即结论③不正确;
④∵∠ABE=∠EBG=30°,∠BGE=∠BAE=90°,
∴∠BEG=∠BGE-∠EBG=90°-30°=60°,
∴∠EBF=∠ABF-∠ABE=90°-30°=60°,
∴∠BFE=180°-60°-60°=60°,
∴∠EBF=∠BEG=∠BFE=60°,
∴△BEF为等边三角形,
即结论④正确;
故答案为:①②④.
点评 此题主要考查了矩形的性质、折叠的性质、等边三角形的判定与性质、梯形的性质等知识;本题综合性强,有一定难度.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
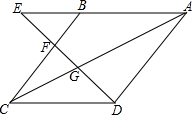 如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.
如图,四边形ABCD是菱形,点E在AB延长线上,联结AC,DE,DE分别交BC,AC于点F,G,且CD•AE=AC•AG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com