
在△ABC中,AB=AC=5,tanB=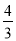 .若⊙O的半径为
.若⊙O的半径为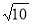 ,且⊙O经过点B、C,那么线段OA的长等于
,且⊙O经过点B、C,那么线段OA的长等于
3或5.
【解析】
试题分析:分两种情况考虑:(i)如图1所示,由AB=AC,OB=OC,利用线段垂直平分线逆定理得到AO垂直平分BC,在直角三角形ABD中,由AB及cos∠ABC的值,利用锐角三角函数定义求出BD的长,再利用勾股定理求出AD的长,在直角三角形OBD中,由OB与BD的长,利用勾股定理求出OD的长,由AD+DO即可求出AO的长;(ii)同理由AD-OD即可求出AO的长,综上,得到所有满足题意的AO的长
试题解析:分两种情况考虑:
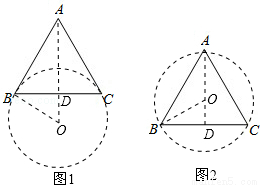
(i)如图1所示,
∵AB=AC,OB=OC,
∴AO垂直平分BC,
∴OA⊥BC,D为BC的中点,
在Rt△ABD中,AB=5,tan∠ABC=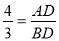 ,
,
设AD=4x,BD=3x,由勾股定理得:(3x)2+(4x)2=52,
x=1,
∴BD=3,AD=4,
在Rt△BDO中,OB=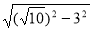 =1,BD=3,
=1,BD=3,
则AO=AD+OD=4+1=5;
(ii)如图2所示,AO=AD-OD=4-1=3;
综合上述,OA的长为3或5.
考点:1.垂径定理;2.等腰三角形的性质;3.解直角三角形.


科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:解答题
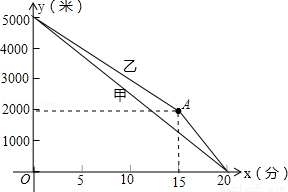
甲、乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答问题:
(1)他们在进行 米的长跑训练,在0<x<15的时段内,速度较快的人是 ;
(2)求甲距终点的路程y(米)和跑步时间x(分)之间的函数关系式;
(3)当x=15时,两人相距多少米?在15<x<20的时段内,求两人速度之差.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市杨浦区5月中考二模数学试卷(解析版) 题型:选择题
将抛物线y=x2-2平移到抛物线y=x2+2x-2的位置,以下描述正确的是( )
A.向左平移1个单位,向上平移1个单位
B.向右平移1个单位,向上平移1个单位
C.向左平移1个单位,向下平移1个单位
D.向右平移1个单位,向下平移1个单位
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:解答题
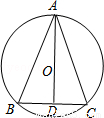
如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年上海市普陀区中考二模数学试卷(解析版) 题型:选择题
下列命题中,错误的是( )
A.三角形重心是三条中线交点 B.三角形外心到各顶点距离相等
C.三角形内心到各边距离相等 D.等腰三角形重心、内心、外心重合
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com