
【题目】一辆轿车从甲地驶往乙地,到达乙地后立即返回甲地,速度是原来的![]() 倍,往返共用
倍,往返共用![]() 小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为
小时.一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶,设轿车行驶的时间为![]() ,两车离开甲地的距离为
,两车离开甲地的距离为![]() ,两车行驶过程中
,两车行驶过程中![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
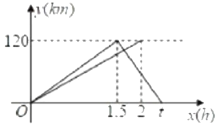
(1)轿车从乙地返回甲地的速度为________![]() ,
,![]() ________;
________;
(2)求轿车从乙地返回甲地时![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当轿车从乙地返回甲地的途中与货车相遇时,求相遇处到甲地的距离.
【答案】(1)![]() ,
,![]()
![]() ;(2)
;(2)![]() ;(3)相遇处到甲地的距离为
;(3)相遇处到甲地的距离为![]()
【解析】
(1)首先根据题意求出轿车从甲地到乙地的速度为![]()
![]() ,由此进一步即可求得轿车从乙地返回甲地的速度为
,由此进一步即可求得轿车从乙地返回甲地的速度为![]()
![]() ,从而得出轿车返回时间为,最后进一步计算即可;
,从而得出轿车返回时间为,最后进一步计算即可;
(2)根据题中所给的函数图像以及(1)中的结论,设出一次函数解析式,利用待定系数法求解即可;
(3)首先根据题意求出货车从甲地前往乙地时![]() 与
与![]() 的函数解析式,结合(2)中求出的解析式联立可得方程组,由此进一步求解即可.
的函数解析式,结合(2)中求出的解析式联立可得方程组,由此进一步求解即可.
(1)轿车从甲地到乙地的速度为:![]()
![]() ,
,
∴轿车从乙地返回甲地的速度为![]()
![]() ,
,
∴轿车返回时间为:![]()
![]() ,
,
∴![]()
![]() ,
,
故答案为:![]() ,
,![]()
![]() ;
;
(2)设轿车从乙地返回甲地时![]() 与
与![]() 函数关系式为
函数关系式为![]()
![]() ,
,
∵函数图像过(1.5,120),(2.5,0),
∴![]() ,
,
解得:![]() ,
,
∴轿车从乙地返回甲地时![]() 与
与![]() 函数关系式为
函数关系式为![]() ;
;
(3)设货车从甲地前往乙地时![]() 与
与![]() 的函数解析式为:
的函数解析式为:![]()
![]() ,
,
∵函数图象过点(2,120),
∴![]() ,
,
∴![]() ,
,
即货车从甲地前往乙地时![]() 与
与![]() 的函数解析式为:
的函数解析式为:![]() ,
,
联立轿车从乙地返回甲地时![]() 与
与![]() 函数关系式可得:
函数关系式可得:![]() ,
,
解得:![]()
∴相遇处到甲地的距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点O为正六边形的中心,P,Q分别从点A(1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2020次相遇地点的坐标为( )
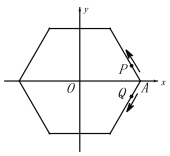
A.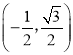 B.
B.![]() C.
C.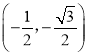 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC与BD相交于点,过点A作AN∥BD,过点B作BN∥AC,两线相交于点N.
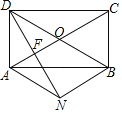
(1)求证:AN=BN;
(2)连接DN,交AC于点F,若DN⊥NB于点N,求∠DOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商贩用600元购进了一批水果,上市后销售非常好,商贩又用1400元购进第二批这种水果,所购水果数量是第一批购进数量的2倍,但每箱进价多了5元.
(1)求该商贩第一批购进水果每箱多少元;
(2)由于储存不当,第二批购进的水果中有10%腐坏,不能售卖,该商贩将两批水果按同一价格全部销售完毕后获利不低于800元,求每箱水果的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
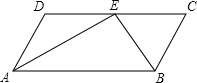
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和即为返现金额.某顾客刚好消费280元,则该顾客所获得返现金额不低于30元的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
(1)如图1,连接![]() ,当
,当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,对角线![]() ,
,![]() 交于点
交于点![]() .连接
.连接![]() ,
,![]() ,若
,若![]() ,试探索
,试探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
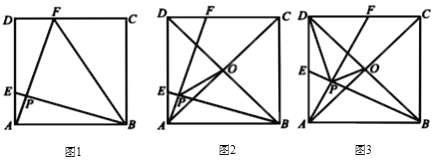
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线B-A-O表示固定支架,AO垂直水平桌面OE于点O,点B为旋转点,BC可转动,当BC绕点B顺时针旋转时,投影探头CD始终垂直于水平桌面OE,经测量:AO=6.4cm,CD=8cm,AB=40cm,BC=45cm,
 图1
图1
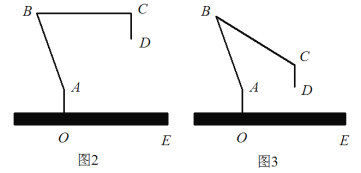
(1)如图2,∠ABC=70°,BC∥OE.
①填空:∠BAO= °
②投影探头的端点D到桌面OE的距离
(2)如图3,将(1)中的BC向下旋转,∠ABC=30°时,求投影探头的端点D到桌面OE的距离
(参考数据:sin70≈0.94,cos70≈0.34,sin40°≈0.64,cos40°≈0.77)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com