
已知A(2,0),直线y=(2−)x−2交x轴于点F,y轴于点B,直线l∥AB且交 y轴于点C,交x轴于点D,点A关于直线l的对称点为A' ,连结AA',A'D。直线l从AB开始,以1个单位每秒的速度沿y轴正方向向上平移,设移动时间为t.
1.求A'点的坐标(用t的代数式表示)
2.请猜想AB与AF长度的数量关系,并说明理由
3.过点C作直线AB的垂线交直线y=(2−)x−2于点E,以点C为圆心CE为半径作⊙C,求当t为何值时,⊙C与△AA′D三边所在直线相切?

1.∵l∥AB. ∴∠ODC=∠OAB
∵A(2, 0) B(0, -2) ∴tan∠OAB=
∴∠ODC=∠OAB=30° ……………1分
∵BC=t, ∴OC=2−t, ∴OD=(2−t) ∴AD=t
∵点A关于直线l的对称点为A',
∴A'D=AD=t ∠A'DA=60° ∴△A'DA是正三角形 ………2分
过点A'作A'H⊥AD于H, ∴AH=t A'H=t
∴A'点的坐标为(2−t, t) ……………3分
2.AB=AF …………4分

说明:∵F(4+2, 0) ∴AF=4
在Rt△OAB中,OA=2, OB=2, ∴AB=4,
∴AB=AF …………6分
3.∵直线l是点A和A'的对称轴

∴直线l是∠A'DA的平分线
∴点C到直线AD和A'D的距离相等
∴当⊙C与AD相切时,也一定与A'D相切…………7分
∵∠OAB=30°且AB=AF
∴∠ABF=15° ∴∠CBF=75°
∵CE⊥AB ∠OBA=60° ∴∠BCE=30°
∴∠CEB=75° ∴CB=CE…………(8分)
∵⊙C与AD相切 ∴OC=CE=CB ∴t=1…………9分
当⊙C与A A'相切于点M时,CE=CB=CM
∴CM=t
∵CM=DM-CD
在Rt△OCD中,∠ODC=30°, OC=t−2
∴CD=2t−4
∴2t−4+t=t ∴t= …………10分
【解析】略


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 是10cm,
是10cm,查看答案和解析>>
科目:初中数学 来源: 题型:
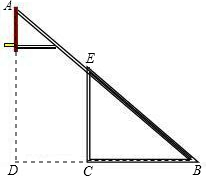
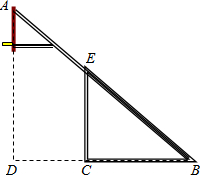 红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
红星中学篮球课外活动小组的同学自己动手制作一副简易篮球架.如图,是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(计算结果精确到0.01米,参考数据:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)查看答案和解析>>
科目:初中数学 来源: 题型:
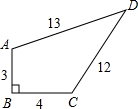 已知一个铁制的实心直四棱柱模型的俯视图如图所示(单位:厘米),它的高是10cm,
已知一个铁制的实心直四棱柱模型的俯视图如图所示(单位:厘米),它的高是10cm,查看答案和解析>>
科目:初中数学 来源: 题型:
曙光中学需制作一副简易篮球架,如图是篮球架的侧面示意图,已知篮板所在直线AD和直杆EC都与BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜杆AB与直杆EC的长分别是多少米?(结果精确到0.01米)
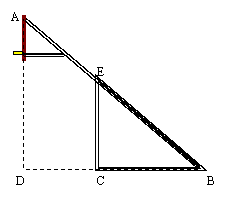 解:
解:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com