
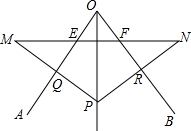
 如图,已知,点P在∠AOB的内,且点P与点N关于OA对称,PM交OA于点Q,点P与点N关于OB对称,PN交OB于点N,MN交OA于点E,MN交OB于点F.
如图,已知,点P在∠AOB的内,且点P与点N关于OA对称,PM交OA于点Q,点P与点N关于OB对称,PN交OB于点N,MN交OA于点E,MN交OB于点F.分析 (1)由轴对称的性质可知ME=PE,FN=PF,从而得到三角形的周长等于MN;
(2)由轴对称的性质可知∠OQP=90°,∠ORP=90°;先求得∠M+∠N=50°,从而得到∠MPE+∠FPE=50°;
(3)根据到角两边距离相等的点在角平分线上进行证明即可.
解答 解:如图连接PE、FP.
(1)∵点P与点M关于OA对称,
∴ME=PE.
同理:FN=PF.
∴△PEF的周长=EP+FP+EF=ME+EF+FN=MN=10;
(2)∵点P与点M关于OA对称,
∴∠OQP=90°.
同理:∠ORP=90°.
由四边形的内角和是360°可知;∠AOB=360°-∠OQP-∠ORP-∠QPR=360°-90°-90°-130°=50°;
∵∠MPN=130°,
∴∠M+∠N=50°.
∵ME=EP,FN=FP,
∴∠M=∠MPE,∠N=∠FPE.
∴∠EPF=130°-50°=80°.
故答案为;50°;80°.
(3)∵PN=PM,Q、R为MP,PN的中点,
∴PQ=PE.
又∵PQ⊥QA,PR⊥OB,
∴OP平分∠AOB.
点评 本题主要考查的是轴对称的性质、多边形的内角和、角平分线的判定,熟练掌握轴对称的性质是解题的关键.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 17 | B. | 26 | C. | 62 | D. | 71 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.
家在四楼的小明从窗口A向楼外掷出一个纸飞机,如果纸飞机下落过程值距离地面的高度h(米)与飞机的水平距离s(米)之间的关系式是h=-$\frac{1}{20}$s2+$\frac{2}{5}$s+m,其图象如图所示,那么这架纸飞机落地处点B与小明家所住的楼的相距20米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,现用三边长分别为a,b,c的四个全等的直角三角形拼成正方形,利用以下方法验证:a2+b2=c2,在图中,边长为c的大正方形的面积为(a2+b2)或c2.
如图所示,现用三边长分别为a,b,c的四个全等的直角三角形拼成正方形,利用以下方法验证:a2+b2=c2,在图中,边长为c的大正方形的面积为(a2+b2)或c2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com