[题目]直角梯形的一个内角为120°.较长的腰为6cm.有一底边长为5cm.则这个梯形的面积为( )A. cm2B. cm2C.25 cm2D. cm2或 cm2 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】直角梯形的一个内角为120°，较长的腰为6cm，有一底边长为5cm，则这个梯形的面积为（）
A. cm2
B. cm2
C.25 cm2
D. cm2或 cm2

【答案】D
【解析】解：根据题意可作出下图，

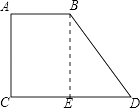
BE为高线，BE⊥CD，即∠A=∠C=90°，∠ABD=120°，BD=6cm，

∵AB∥CD，∠ABD=120°，

∴∠D=60°，

∴BE=6×sin60°=3 cm；ED=6×cos60°=3cm；

当AB=5cm时，CD=5+3=8cm，梯形的面积= ×（5+8）×3 = cm2；

当CD=5cm时，AB=5﹣3=2cm，梯形的面积= ×（2+5）×3 = cm2；

故梯形的面积为 cm2或 cm2，
所以答案是：D．

【考点精析】关于本题考查的直角梯形和锐角三角函数的定义，需要了解一腰垂直于底的梯形是直角梯形；锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能得出正确答案．

练习册系列答案

天利38套初中名校期末联考测试卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】（1）的立方根是______________．

（2）已知某正数的两个平方根分别是a+3和2a-15，b的立方根是-2，则3a+b的算术平方根是___________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】完成下面推理过程：

如图，已知∠1 ＝∠2，∠B ＝∠C，可推得AB∥CD．理由如下：

∵∠1 ＝∠2（已知），

且∠1 ＝∠CGD（______________ _________），

∴∠2 ＝∠CGD（等量代换）．

∴CE∥BF（___________________ ________）．

∴∠ ＝∠C（__________________________）．

又∵∠B ＝∠C（已知），

∴∠ ＝∠B（等量代换）．

∴AB∥CD（________________________________）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，轮船沿正南方向以33海里/时的速度匀速航行，在m处观测到灯塔p在西偏南69°方向下，航行2小时后到达n处，观测灯塔p在西偏南57°方向上，若该船继续向南航行至离灯塔最近位置，求此时轮船离灯塔的距离约为多少海里？（结果精确到整数，参考数据：tan33°≈ ，sin33°≈ ，cos33°≈ ，tan21°≈ ，sin21°≈ ，c0s21°≈ ）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】问题的提出：n个平面最多可以把空间分割成多少个部分？
问题的转化：由n上面问题比较复杂，所以我们先来研究跟它类似的一个较简单的问题：
n条直线最多可以把平面分割成多少个部分？
如图1，很明显，平面中画出1条直线时，会得到1+1=2个部分；所以，1条直线最多可以把平面分割成2个部分；
如图2，平面中画出第2条直线时，新增的一条直线与已知的1条直线最多有1个交点，这个交点会把新增的这条直线分成2部分，从而多出2个部分，即总共会得到1+1+2=4个部分，所以，2条直线最多可以把平面分割成4个部分；
如图3，平面中画出第3条直线时，新增的一条直线与已知的2条直线最多有2个交点，这2个交点会把新增的这条直线分成3部分，从而多出3个部分，即总共会得到1+1+2+3=7个部分，所以，3条直线最多可以把平面分割成7个部分；
平面中画出第4条直线时，新增的一条直线与已知的3条直线最多有3个交点，这3个交点会把新增的这条直线分成4部分，从而多出4个部分，即总共会得到1+1+2+3+4=11个部分，所以，4条直线最多可以把平面分割成11个部分；…

（1）请你仿照前面的推导过程，写出“5条直线最多可以把平面分割成多少个部分”的推导过程（只写推导过程，不画图）；
（2）根据递推规律用n的代数式填空：n条直线最多可以把平面分割成个部分．
问题的解决：借助前面的研究，我们继续开头的问题；n个平面最多可以把空间分割成多少个部分？
首先，很明显，空间中画出1个平面时，会得到1+1=2个部分；所以，1个平面最多可以把空间分割成2个部分；
空间中有2个平面时，新增的一个平面与已知的1个平面最多有1条交线，这1条交线会把新增的这个平面最多分成2部分，从而多出2个部分，即总共会得到1+1+2=4个部分，所以，2个平面最多可以把空间分割成4个部分；
空间中有3个平面时，新增的一个平面与已知的2个平面最多有2条交线，这2条交线会把新增的这个平面最多分成4部分，从而多出4个部分，即总共会得到1+1+2+4=8个部分，所以，3个平面最多可以把空间分割成8个部分；
空间中有4个平面时，新增的一个平面与已知的3个平面最多有3条交线，这3条交线会把新增的这个平面最多分成7部分，从而多出7个部分，即总共会得到1+1+2+4+7=15个部分，所以，4个平面最多可以把空间分割成15个部分；
空间中有5个平面时，新增的一个平面与已知的4个平面最多有4条交线，这4条交线会把新增的这个平面最多分成11部分，而从多出11个部分，即总共会得到1+1+2+4+7+11=26个部分，所以，5个平面最多可以把空间分割成26个部分；…
（3）请你仿照前面的推导过程，写出“6个平面最多可以把空间分割成多少个部分？”的推导过程（只写推导过程，不画图）；
（4）根据递推规律填写结果：10个平面最多可以把空间分割成个部分；
（5）设n个平面最多可以把空间分割成Sn个部分，设n﹣1个平面最多可以把空间分割成Sn﹣1个部分，前面的递推规律可以用Sn﹣1和n的代数式表示Sn；这个等式是Sn= ．