
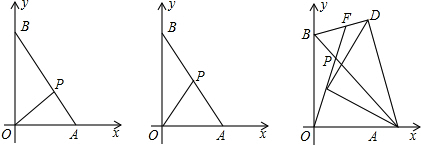
���� ��1���Ե�ʽ���������Ӷ�������ߵij����ɷ�������Ϲ��ɶ������涨����������ֱ�������Σ���һ�����������ε�����������������ϵĸߣ�б���ϵĸߣ���
��2���ӳ�CD��E��ʹDE=CD������AE��BE�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı����жϳ��ı���AEBC��ƽ���ı��Σ��ٸ�����һ������ֱ�ǵ�ƽ���ı����Ǿ��οɵ��ı���AEBC�Ǿ��Σ�Ȼ����ݾ��εĶԽ�����ƽ������ȿɵ�OP=$\frac{1}{2}$AB��
��3����ͼ3����B��BM��OF��M����D��DN��OF��OF�ӳ�����N������ȫ�������Σ���MOB�ա�NED����MFB�ա�NFD�����ȫ�������εĶ�Ӧ�������֪BF=FD���ɣ�
��� 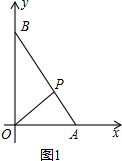 �⣺��1����ͼ1����a2+b2+c2-6a-8b-10c+50=0��
�⣺��1����ͼ1����a2+b2+c2-6a-8b-10c+50=0��
�ࣨa-3��2+��b-4��2+��c-5��2=0��
��a=3��b=4��c=5��
��$\frac{1}{2}$ab=$\frac{1}{2}$c•OP��
��OP=$\frac{12}{5}$��
��2��OP=$\frac{1}{2}$AB���������£�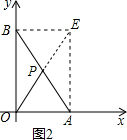
��ͼ2���ӳ�OP��E�㣬ʹPE=OP����BE��AE��
��OP��б��AB�ϵ����ߣ�
��AP=BP��
���ı���OAEB��ƽ���ı��Σ�
�ߡ�AOB=90�㣬
���ı���OAEB�Ǿ��Σ�
��AP=BP=OP=PE��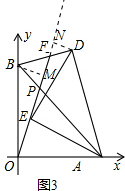
��OP=$\frac{1}{2}$AB��
��3��֤������ͼ3����B��BM��OF��M����D��DN��OF��OF�ӳ�����N��
�ߡ�AOE=��AEO����AOE+��BOM=��AEO+��DEN=90��
���BOM=��DEN��
�ڡ�MOB���NED�У�
$\left\{\begin{array}{l}{��BMO=��NDE=90��}\\{��BOM=��DEN}\\{OB=ED}\end{array}\right.$��
��֤��MOB�ա�NED��AAS����
��BM=DN��
ͬ����֤��MFB�ա�NFD��
��BF=FD��
��$\frac{BF}{FD}$=1��
���� ���⿼�����������ۺ��⣬����ʱ��������ʽ�ֽ��Ӧ�ã������䷽��������ȫƽ����ʽ���Ǹ��������ʺ��ɶ����涨���������ε�������������ͨ���������߹������Σ�ȫ���������ǽ�����ѵ㣮ͬʱ���鴦���ۺ�������������ѶȽϴ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
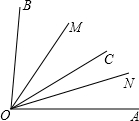 ��ͼ����֪��AOB=84�㣬OM��ON�ֱ��ǡ�BOC�͡�AOC��ƽ���ߣ�
��ͼ����֪��AOB=84�㣬OM��ON�ֱ��ǡ�BOC�͡�AOC��ƽ���ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���ۣ�Ԫ/���� | 30 | 34 | 38 | 40 | 42 |
| ���������� | 40 | 32 | 24 | 20 | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����˫����y=$\frac{k}{x}$��߳�Ϊ5�ĵȱߡ�AOB�ı�OA��AB�ֱ��ཻ��C��D���㣬��OC=3BD����ʵ��k��ֵΪ$\frac{9\sqrt{3}}{4}$��
��ͼ����˫����y=$\frac{k}{x}$��߳�Ϊ5�ĵȱߡ�AOB�ı�OA��AB�ֱ��ཻ��C��D���㣬��OC=3BD����ʵ��k��ֵΪ$\frac{9\sqrt{3}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
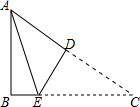 ��ͼ��ʾ���ڡ�ABC�У���B=90�㣬AB=3��AC=5���߶�AC�Ĵ�ֱƽ����DE��AC��D��BC��E�����ABE���ܳ�Ϊ7��
��ͼ��ʾ���ڡ�ABC�У���B=90�㣬AB=3��AC=5���߶�AC�Ĵ�ֱƽ����DE��AC��D��BC��E�����ABE���ܳ�Ϊ7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
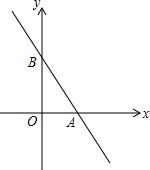 ��֪һ�κ���y=kx+bͼ����x�ᡢy��Ľ���ΪA��B���㣬�ҵ�x=1��y=2����x=-1��y=6��
��֪һ�κ���y=kx+bͼ����x�ᡢy��Ľ���ΪA��B���㣬�ҵ�x=1��y=2����x=-1��y=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{5}$ | B�� | $\frac{4\sqrt{5}}{5}$ | C�� | 2$\sqrt{5}$ | D�� | $\frac{2\sqrt{5}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com