
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,将
边上一点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.连结
处.连结![]() ,当
,当![]() 为直角三角形时,
为直角三角形时,![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】D
【解析】
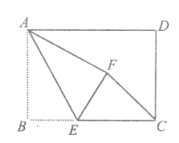
当△CEF为直角三角形时,有两种情况:①当点F落在矩形内部时,如图1所示.连结AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AFE=∠B=90°,而当△CEF为直角三角形时,只能得到∠EFC=90°,所以点 A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,则EB=EF,AB=AF=6,可计算出CF=4,设BE=x,则EF=x,CE=8-x,然后在Rt△CEF中运用勾股定理可计算出x.②当点F落在AD边上时,如图2所示.此时四边形ABEF为正方形.
解:当△CEF为直角三角形时,有两种情况:
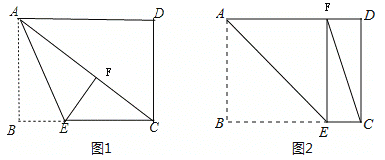
①当点F落在矩形内部时,如图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC=![]() =10,
=10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,如图,
∴EB=EF,AB=AF=6,
∴CF=10-6=4,
设BE=x,则EF=x,CE=8-x,
在Rt△CEF中,
∵EF2+CF2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴BE=3;
②当点F落在AD边上时,如图2所示.
此时ABEF为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故选D.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
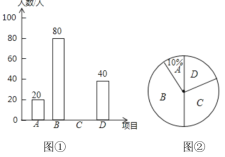
【题目】运城市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:
A.绿化造林 B.汽车限行 C.拆除燃煤小锅炉 D.使用清洁能源.
调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整.
(3)求图2中![]() 项目对应的扇形的圆心角的度数.
项目对应的扇形的圆心角的度数.
(4)请你结合自己的实际情况对有效治理雾霾提几点建议.(至少写一条)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、…、,按一定规律排成如表:
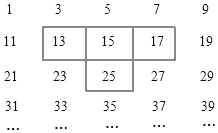
图中的T字框框住了四个数字,若将T字框上下左右移动,按同样的方式可框住另外的四个数, 若将T字框上下左右移动,则框住的四个数的和不可能得到的数是( )
A.22B.70C.182D.206
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
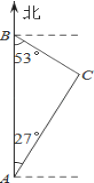
【题目】如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
(参考数据:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO,交AD于点F,OE⊥OB交BC于点E.
(1)如图1,当O为边AC中点,![]() 时,求
时,求![]() 的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案
的值.小明这样想的,过O点作OH∥AB交BC于点H,可证△AOF∽△HOE,于是求出答案,请你直接写出答案![]() ;
;
(2)如图2,当O为边AC中点,![]() 时,请求出
时,请求出![]() 的值,并说明理由;
的值,并说明理由;
(3)如图3,当![]() ,
,![]() 时,请直接写出
时,请直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是长方体的平面展开图,设![]() ,若
,若![]() .
.
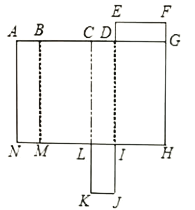
(1)求长方形![]() 的周长与长方形
的周长与长方形![]() 的周长(用字母
的周长(用字母![]() 进行表示) ;
进行表示) ;
(2)若长方形![]() 的周长比长方形
的周长比长方形![]() 的周长少8,求原长方体的体积.
的周长少8,求原长方体的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
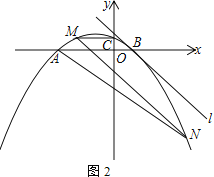
【题目】已知:抛物线y=a(x-m)(x+3m)(a<0,m>0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线l:y=kx+b经过点B,且与该抛物线有唯一公共点,平移直线l交抛物线于M、N两点(点M、N分别位于x轴上方和下方)
(1) 若![]() ,C(0,
,C(0,![]() )
)
① 求该抛物线的解析式
② 如图1,连接AM、AN,求证:∠MAB=∠NAB
(2) 如图2,连接MC.若MC∥x轴,求![]() 的值
的值

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com