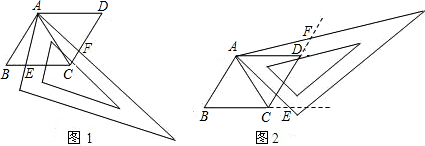
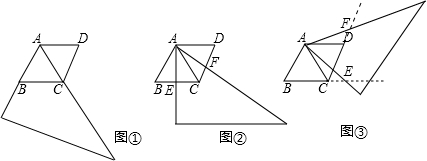
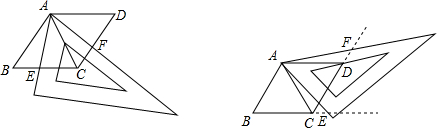
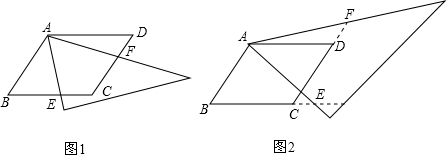
解:(1)①BE=CF;
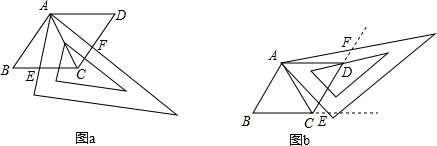
②∵菱形ABCD由等边△ABC和△ACD拼成,
∴AB=AC,∠B=∠CAB=∠ACD=60°,
而∠FAE=60°,
∴∠BAE=60°-∠CAE=∠CAF,
在△BAE和△CAF中
∵
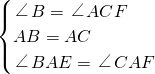
∴△BAE≌△CAF,
∴BE=CF;
(2)△AEF为等边三角形.
理由如下:

连EF,
∵菱形ABCD由等边△ABC和△ACD拼成,
∴AC=AD,∠ACB=∠ADC=∠CAD=60°,
∴∠ACE=120°,∠ADF=120°,
∴∠ACE=∠ADF,
而∠FAE=60°,
∴∠CAE=60°-∠DAE=∠DAF,
在△ACE和△ADF中
∵

∴△ACE≌△ADF,
∴AE=AF,
∴△AEF为等边三角形.
分析:(1)①BE=CF;②由于菱形ABCD由等边△ABC和△ACD拼成,根据等边三角形的性质得到AB=AC,∠B=∠CAB=∠ACD=60°,而∠FAE=60°,得到∠BAE=60°-∠CAE=∠CAF,根据全等三角形的判定方法易得△BAE≌△CAF,即可得到BE=CF;
(2)由于菱形ABCD由等边△ABC和△ACD拼成,根据等边三角形的性质得到AC=AD,∠ACB=∠ADC=∠CAD=60°,则∠ACE=120°,∠ADF=120°,得到∠ACE=∠ADF,
而∠FAE=60°,得到∠CAE=60°-∠DAE=∠DAF,根据全等三角形的判定方法易得△ACE≌△ADF,则AE=AF,根据等边三角形的判定方法即可得到△AEF为等边三角形.
点评:本题考查了旋转的性质:旋转前后两图形全等,即对应线段相等,对应角相等,对应点与旋转中心的连线段的夹角等于旋转角.也考查了全等三角形的判定与性质以及等边三角形的判定与性质.

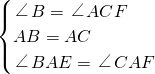
 连EF,
连EF,