
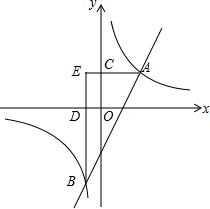
 ��ͼ��˫����y=
��ͼ��˫����y=| k |
| x |
| 5 |
| k |
| x |
| MB | ||
|
| MB | ||
|
| MA |
| 1 |
| k |
| x |
|
|
|
|

| AE2+BE2 |
| 9+36 |
| 5 |
| DH |
| AE |
| BD |
| BA |
| DH |
| 3 |
| 4 | ||
3
|
4
| ||
| 5 |
4
| ||
| 5 |
| EF2+BE2 |
| 32+62 |
| 5 |
| MG |
| MB |
| FE |
| FB |
| 3 | ||
3
|
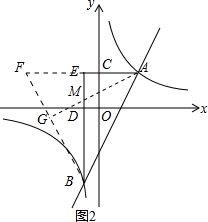
| MB | ||
|
| MB | ||
|
| MA |
| 1 |
| EM |
| EF |
| AE |
| BE |
| EM |
| 3 |
| 3 |
| 6 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| MB | ||
|
| MA |
| 1 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ�������е�С�����εı߳�Ϊ��Ϊ1���밴Ҫ��������е����⣺�ڷ���ֽ�л�һ�����Ϊ5��Rt��ABC��һ�����Ϊ5��������EFGH��
��ͼ�������е�С�����εı߳�Ϊ��Ϊ1���밴Ҫ��������е����⣺�ڷ���ֽ�л�һ�����Ϊ5��Rt��ABC��һ�����Ϊ5��������EFGH���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| c |
. |
| a |
. |
| b |
. |
| c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
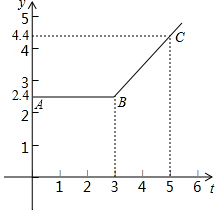 ͼ�е�����ABCΪ�Ӽ����ҵش�;�绰���踶�ĵ绰��y��Ԫ����ͨ��ʱ��t�����ӣ�֮��仯��ϵ��ͼ��
ͼ�е�����ABCΪ�Ӽ����ҵش�;�绰���踶�ĵ绰��y��Ԫ����ͨ��ʱ��t�����ӣ�֮��仯��ϵ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
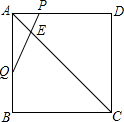 ��ͼ��������ABCD�У���PΪ��AD��һ�㣬DP=3AP����QΪ��AB���е㣬����PQ���Խ���AC�ڵ�E������
��ͼ��������ABCD�У���PΪ��AD��һ�㣬DP=3AP����QΪ��AB���е㣬����PQ���Խ���AC�ڵ�E������| PE |
| EQ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
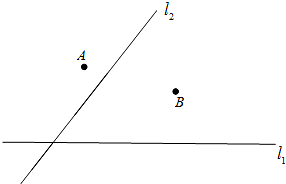 �ڹ�·l1ͬ�ࡢl2������������A��B������ͼ�����Ų���Ҫ��һ���źŷ��������������Ҫ����������������A��B�ľ��������ȣ���������·l1��l2�ľ���Ҳ������ȣ�������CӦ����ʲôλ�ã����ó߹���ͼ�ҳ����з��������ĵ㣬ע����C��λ�ã�
�ڹ�·l1ͬ�ࡢl2������������A��B������ͼ�����Ų���Ҫ��һ���źŷ��������������Ҫ����������������A��B�ľ��������ȣ���������·l1��l2�ľ���Ҳ������ȣ�������CӦ����ʲôλ�ã����ó߹���ͼ�ҳ����з��������ĵ㣬ע����C��λ�ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com