
分析 (1)①×2-②得出-x=-6,求出x,把x=6代入①求出y即可;
(2)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=0①}\\{3x+4y=6②}\end{array}\right.$
①×2-②得:-x=-6,
解得:x=6,
把x=6代入①得:6+2y=0,
解得:y=-3,
所以方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=-3}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{5x-9<3(x-1)①}\\{1-\frac{3}{2}x≤\frac{1}{2}x-1②}\end{array}\right.$
∵解不等式①得:x<3,
解不等式②得:x≥1,
∴不等式组的解集,1≤x<3.
点评 本题考查了解一元一次不等式组,解二元一次方程组等知识点,能把二元一次方程组转化成一元一次方程是解(1)的关键,能求出不等式组的解集是解(2)的关键.


科目:初中数学 来源: 题型:解答题
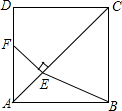 如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.
如图,在正方形ABCD中,点E是对角线AC上一点,且CE=CD,过点E作EF⊥AC交AD于点F,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
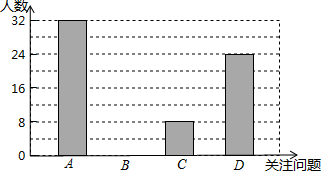 6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:
6月5日是世界环境日,2017年世界环境日中国的主题是“绿水青山就是金山银山”,小明积极学习与宣传,并从四个方面(A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖)对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),并绘制了如下不完整的统计图表:| 关注的问题 | 频数 | 频率 |
| A | 32 | m |
| B | a | 0.2 |
| C | 8 | 0.1 |
| D | 24 | n |
| 合计 | b | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
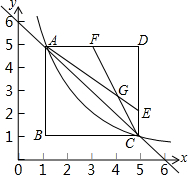 如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.
如图,若直线y=-x+6与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A(1,m)与C(n,1)两点,以线段AC为斜边,在AC的两侧作等腰直角三角形ABC和ADC,其中∠B=∠D=90°,F为AD的中点,点E在边CD上,且DE=3EC,AE与CF相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com