
解:(1)
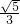
(2)

图形、已知、求证和证明过程如下:
已知:在△ABC中,AB=AC,EF∥BC,⊙O内切于梯形EBCF,点D、N、G、M为切点,
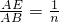
(n是大于1的自然数)
求证:sinB=

.
证法一:
连接AO并延长与BC相交
∵⊙O内切于梯形EBCF,AB、AC是⊙O的切线,
∴∠BAO=∠CAO.
∵EF∥BC,AB=AC,
∴AE=AF.
又M、N为切点,
∴OM⊥EF,ON⊥BC,
∴AO⊥EF于M,AO⊥BC于N.
∵EF∥BC,∴EM∥BN.
∴△AEM∽△ABN.
∴

.
设EM=k,则BN=nk.
作EH∥MN交BC于H,则HN=EM=k.
∵D、N、M为切点,
∴BD=BN=nk,ED=EM=k.
在△EHB中,∠EHB=∠MNB=90°,
BE=BD+DE=(n+1)k,
BH=BN-HN=(n-1)k,
由勾股定理得EH=2

•k
∴sinB=

.
证法二:
接证法一中,∵EF∥BC,∴EM∥BN
∴
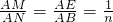
.
设AM=k,则AN=nk,MN=(n-1)k.
连接OD,∵D为切点,∴OD⊥AB
∴OM=OD=

MN=

,OA=AM+MO=
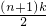
在Rt△AOD中,由勾股定理得AD=

•k
∵∠B+∠BAN=∠AOD+∠BAN=90°,
∴∠B=∠AOD
∴sinB=sin∠AOD=

.
分析:(1)
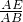
的分母加1即是sinB的分母,sinB的分子是2乘以
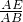
的分母的算术平方根,根据规律直接写出答案即可;
(2)由已知条件先写出已知和求证,再进行证明:
要想表示出sinB,需证明△AEM∽△ABN,得出

,再设EM=k,则BN=nk,作EH∥MN交BC于H,则HN=EM=k.
由勾股定理得EH=2

•k,则sinB=

.
点评:本题考查的是切割线定理,切线的性质定理,勾股定理.

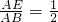 时,sinB=
时,sinB=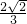 ;
;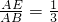 时,sinB=
时,sinB= (提示:
(提示: =
=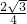 );
);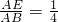 时,sinB=
时,sinB= .
.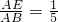 时,sinB的值等于______;
时,sinB的值等于______;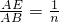 时(n是大于1的自然数),请用含n的代数式表示sinB=______,并画出图形,写出已知、求证和证明过程.
时(n是大于1的自然数),请用含n的代数式表示sinB=______,并画出图形,写出已知、求证和证明过程. 解:(1)
解:(1)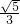

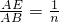 (n是大于1的自然数)
(n是大于1的自然数) .
. .
. •k
•k .
.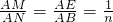 .
. MN=
MN= ,OA=AM+MO=
,OA=AM+MO=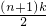
 •k
•k .
.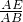 的分母加1即是sinB的分母,sinB的分子是2乘以
的分母加1即是sinB的分母,sinB的分子是2乘以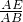 的分母的算术平方根,根据规律直接写出答案即可;
的分母的算术平方根,根据规律直接写出答案即可; ,再设EM=k,则BN=nk,作EH∥MN交BC于H,则HN=EM=k.
,再设EM=k,则BN=nk,作EH∥MN交BC于H,则HN=EM=k. •k,则sinB=
•k,则sinB= .
.

 时,sinB=
时,sinB=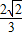 ;
;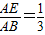 时,sinB=
时,sinB=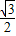 (提示:
(提示: =
=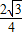 );
);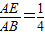 时,sinB=
时,sinB= .
. 时,sinB的值等于______
时,sinB的值等于______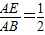 时,sinB=
时,sinB=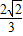 ;
; 时,sinB=
时,sinB=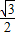 (提示:
(提示: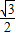 =
=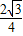 );
);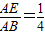 时,sinB=
时,sinB= .
.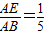 时,sinB的值等于______
时,sinB的值等于______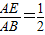 时,sinB=
时,sinB= ;
;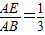 时,sinB=
时,sinB= (提示:
(提示: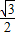 =
=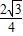 );
); 时,sinB=
时,sinB= .
.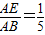 时,sinB的值等于______
时,sinB的值等于______