
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和( ,
, )两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
(1)求a,b,c的值;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
(1)a= ,b=c=0;(2)证明见解析;(3)P的纵坐标为0或4+2
,b=c=0;(2)证明见解析;(3)P的纵坐标为0或4+2 或4﹣2
或4﹣2 .
.
解析试题分析:(1)根据题意得出二次函数一般形式进而将已知点代入求出a,b,c的值即可;
(2)设P(x,y),表示出⊙P的半径r,进而与 x2比较得出答案即可;
x2比较得出答案即可;
(3)分别表示出AM,AN的长,进而分别利用当AM=AN时,当AM=MN时,当AN=MN时,求出a的值,进而得出圆心P的纵坐标即可.
试题解析:(1)∵抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和( ,
, )两点,
)两点,
∴抛物线的一般式为:y=ax2,
∴ =a(
=a( )2,
)2,
解得:a=± ,
,
∵图象开口向上,∴a= ,
,
∴抛物线解析式为:y= x2,
x2,
故a= ,b=c=0;
,b=c=0;
(2)设P(x,y),⊙P的半径r= ,
,
又∵y= x2,则r=
x2,则r= ,
,
化简得:r= >
> x2,
x2,
∴点P在运动过程中,⊙P始终与x轴相交;
(3)设P(a, a2),∵PA=
a2),∵PA= ,
,
作PH⊥MN于H,则PM=PN= ,
,
又∵PH= a2,
a2,
则MH=NH= =2,
=2,
故MN=4,
∴M(a﹣2,0),N(a+2,0),
又∵A(0,2),∴AM= ,AN=
,AN= ,
,
当AM=AN时, =
= ,
,
解得:a=0,
当AM=MN时, =4,
=4,
解得:a=2±2 (负数舍去),则
(负数舍去),则 a2=4+2
a2=4+2 ;
;
当AN=MN时, =4,
=4,
解得:a=﹣2±2 (负数舍去),则
(负数舍去),则 a2=4﹣2
a2=4﹣2 ;
;
综上所述,P的纵坐标为0或4+2 或4﹣2
或4﹣2 .
.
考点:二次函数综合题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:填空题
如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 cm。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线 经过点A和点C,对称轴为直线l:
经过点A和点C,对称轴为直线l: ,该抛物线与x轴的另一个交点为B.
,该抛物线与x轴的另一个交点为B.
(1)求此抛物线的解析式;
(2)点P在直线l上,求出使△PAC的周长最小的点P的坐标;
(3)点M在此抛物线上,点N在y轴上,以A、B、M、N为顶点的四边形能否为平行四边形?若能,直接写出所有满足要求的点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线y=x2﹣(k+2)x+ 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)抛物线于x轴交于点A、B,直线与x轴交于点C,设A、B、C三点的横坐标分别是x1、x2、x3,求x1•x2•x3的最大值;
(3)如果抛物线与x轴的交点A、B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D、E,直线AD交直线CE于点G(如图),且CA•GE=CG•AB,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ,A(3,0),D(-1,0),E(0,3).
,A(3,0),D(-1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.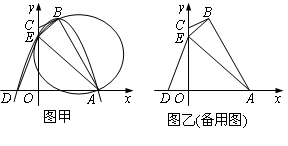
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,二次函数y= x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式.
(2)求函数图象的顶点坐标及D点的坐标.
(3)该二次函数的对称轴交x轴于C点.连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积.
(4)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在S△ADP= S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
S△BCD?若存在,请求出P点的坐标;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
己知:二次函数y=ax2+bx+6(a≠0)与x轴交于A、B两点(点A在点B的左侧)点
A、点B的横坐标是一元二次方程x2-4x-12=0的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使△APC的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段0B上一个动点(点Q不与点0、B重合).过点Q作QD∥AC交BC于点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在等腰△ABC中,底边BC=8,高AD=2,一动点Q从B点出发,以每秒1个单位的速度沿BC向右运动,到达D点停止;另一动点P从距离B点1个单位的位置出发,以相同的速度沿BC向右运动,到达DC中点停止;已知P、Q同时出发,以PQ为边作正方形PQMN,使正方形PQMN和△ABC在BC的同侧,设运动的时间为t秒(t≥0).
(1)当点N落在AB边上时,t的值为 ,当点N落在AC边上时,t的值为 ;
(2)设正方形PQMN与△ABC重叠部分面积为S,求出当重叠部分为五边形时S与t的函数关系式以及t的取值范围;
(3)(本小题选做题,做对得5分,但全卷不超过150分)
如图2,分别取AB、AC的中点E、F,连接ED、FD,当点P、Q开始运动时,点G从BE中点出发,以每秒 个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
个单位的速度沿折线BE-ED-DF向F点运动,到达F点停止运动.请问在点P的整个运动过程中,点G可能与PN边的中点重合吗?如果可能,请直接写出t的值或取值范围;若不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com