

���� ��1������Q��QM��BC���ֱ����AQ��BP�ij�����Rt��QPM�У����ݹ��ɶ����ó�QP�ij����ɣ�
��2��D��Q�������������ͬ��P��C�������������ͬ���ĵ���ͬһ��������˵�����ǵĶԳ�����һ���ģ�д���ĵ�����꣬�ٷֱ�������ǵĶԳ��ἴ�ɵý⣻
��3�������AQ��BP�ij�������Բ�����ı��εĶԱߺ�����Լ����ɶ������н�𣬾ݴ˼��ɵý⣮
��� �⣺��1����ͼ1������Q��QM��BC�� ����ֱ������ABCD�У�AD��BC����A=90�㣬
����ֱ������ABCD�У�AD��BC����A=90�㣬
���ı���ABMQ�Ǿ��Σ�
��QM=AB=12��
��t=6ʱ��DQ=6��AQ=16-6=10��BP=3��6=18��
��BM=AQ=10��
��PM=18-10=8��
��Rt��PQM�У���PMQ=90�㣬PM=8��QM=12��
QP=$\sqrt{{8}^{2}+1{2}^{2}}$=$\sqrt{208}$=4$\sqrt{13}$��
��2����ͼ2��ʾ��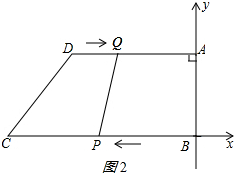
DQ=t��AQ=16-t��BP=3t��BC=21��AD=16��
��D��-16��12����Q��t-16��12����C��-21��0����P��-3t��0����
D��Q����ĶԳ���Ϊ��$\frac{-16+t-16}{2}$��
C��P����ĶԳ���Ϊ��$\frac{-21-3t}{2}$��
��D��Q��P��C�ĵ���ͬһ�������ϣ�
��$\frac{-16+t-16}{2}=\frac{-21-3t}{2}$��
��ã�t=$\frac{11}{4}$��
��t=$\frac{11}{4}$ʱ��D��Q��P��C�ĵ���ͬһ�������ϣ�
��3����ͼ3��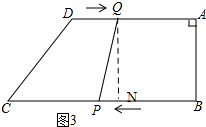 ����Q��QN��BC������ΪN��
����Q��QN��BC������ΪN��
����ֱ������ABCD�У�AD��BC����A=90�㣬
���ı���ABNQ�Ǿ��Σ�
��QN=AB=12��BN=AQ=16-t��BP=3t��
���ı���ABPQΪԲ�����ı��Σ�
��AQ+BP=PQ+AB��
��PQ=16-t+3t-12=2t+4��PN=3t-��16-t��=4t-16��
��Rt��PNQ��PQ2=PN2+QN2��
������2t+4��2=��4t-16��2+122��
��ã�t=4��t=8���ᣩ��
�൱t=4ʱ���ı���ABPQΪԲ�����ı��Σ�
���� �������ı����ۺ���Ŀ����Ҫ�����˶������⡢���ɶ�����Բ�������ı��εĶԱߺ���ȵ�֪ʶ�㣻����������⣬�ڵ���������ʶ����P��7���ֹͣ�ǽ���Ĺؼ���Ҫע�������ܽᣮ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ֱ��������ABC�У���ACB=90�㣬��A����B����C�ĶԱ߷ֱ���a��b��c��CD��AB�ڵ�D����AC=8��BC=6����AB��AD��BD�ij��Լ�������ABC�������
��ֱ��������ABC�У���ACB=90�㣬��A����B����C�ĶԱ߷ֱ���a��b��c��CD��AB�ڵ�D����AC=8��BC=6����AB��AD��BD�ij��Լ�������ABC��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=ax2+bx+c��a��0��c��0����x���ڵ�A��B����y���ڵ�C�������A��B��C��Բ��y�����һ������ΪD����֪��A��B��C������ֱ�Ϊ��-2��0������8��0������0��-4����
��ͼ����֪������y=ax2+bx+c��a��0��c��0����x���ڵ�A��B����y���ڵ�C�������A��B��C��Բ��y�����һ������ΪD����֪��A��B��C������ֱ�Ϊ��-2��0������8��0������0��-4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 102�� | B�� | 104�� | C�� | 106�� | D�� | 108�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
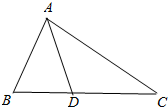 ��ͼ���ڡ�ABC�У�D��BC���ϵĵ㣬AD=DC����BAD=40�㣬��C=35�㣬��֤����ABD�ǵ��������Σ�
��ͼ���ڡ�ABC�У�D��BC���ϵĵ㣬AD=DC����BAD=40�㣬��C=35�㣬��֤����ABD�ǵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ABC�У�D��AC��һ�㣬AD��DC=2��1��BD=$\sqrt{3}$+1����ADB=60�㣬��C=45�㣬���ж�ֱ��AB���BCD�����Բ���ཻ�������У���֤����Ľ��ۣ�
��ABC�У�D��AC��һ�㣬AD��DC=2��1��BD=$\sqrt{3}$+1����ADB=60�㣬��C=45�㣬���ж�ֱ��AB���BCD�����Բ���ཻ�������У���֤����Ľ��ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com