
 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
分析 (1)根据题意利用勾股定理表示出AD2的值,进而得出等式求出答案;
(2)根据题意利用勾股定理表示出FG2的值,进而得出等式求出答案.
解答 解:(1)如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则CD=14-x,
由勾股定理得:AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
故152-x2=132-(14-x)2,
解得:x=9.
∴AD=12.
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×14×12=84.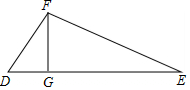 (2)如图,在△DEF中,DE=15,EF=13,DF=4,
(2)如图,在△DEF中,DE=15,EF=13,DF=4,
设GD=x,则GE=15-x,
由勾股定理得:FG2=DF2-GD2=42-x2,FG2=EF2-EG2=132-(15-x)2,
故42-x2=132-(15-x)2,
解得:x=2.4.
∴FG=3.2.
∴S△DEF=$\frac{1}{2}$DE•FG=$\frac{1}{2}$×15×3.2=24.
故答案为:24.
点评 此题主要考查了勾股定理,根据题意正确表示出AD2,FG2的值是解题关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
| A型 | B型 | |
| 价格(万元/台) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a+3b=1 | B. | 3a+2b=-11 | C. | a+b=2 | D. | a-b=-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
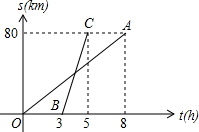 如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
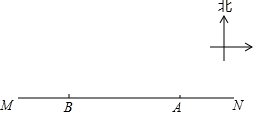 舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.
舟山市朱家尖南沙是一处游泳避暑的好地方.海岸线MN上有两个观察台A、B,A在B的正东方向,AB=400米.从A测得一个游泳者在北偏西60°方向,从B测得这个游泳者在北偏东45°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com