
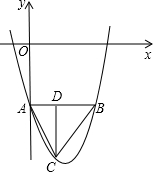
 如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).
如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).分析 (1)根据顶点坐标(2,-9),设出抛物线顶点形式,将(0,-5)代入求出a的值,即可确定出抛物线解析式;
(2)①先根据当y=-5时,-5=x2-4x-5,求得B(4,-5),再分两种情况讨论:当0<m<4时,点C在AB的下方的抛物线上;当4≤m≤5时,点C在抛物线上,分别求得s关于m的函数解析式;②分两种情况,求得当点C与抛物线与x轴交点重合时,△ABC的面积最大,最大面积为10.
解答 解:(1)设二次函数的解析式为y=a(x-h)2+k,
∵顶点坐标(2,-9)
∴y=a(x-2)2-9,
将点A(0,-5)代入,得
-5=4a-9,
解得a=1,
∴抛物线解析式为y=(x-2)2-9=x2-4x-5;
(2)①当y=-5时,-5=x2-4x-5,
解得x1=0,x2=4,
∴B(4,-5),
∵点M的横坐标为m,且0<m≤5,
∴当0<m<4时,点C在AB的下方的抛物线上,
设C(m,m2-4m-5),则
△ABC的面积=$\frac{1}{2}$×AB×CD,即s=$\frac{1}{2}$×4×[-5-(m2-4m-5)]=2(-m2+4m)=-2m2+8m(0<m<4);
当4≤m≤5时,点C在抛物线上,
△ABC的面积=$\frac{1}{2}$×AB×CD,即s=$\frac{1}{2}$×4×[m2-4m-5-(-5)]=2(m2-4m)=2m2-8m(4≤m≤5);
综上所述,s关于m的函数解析式为s=$\left\{\begin{array}{l}{-2{m}^{2}+8m\\;(0<m<4)}\\{2{m}^{2}-8m\\;(4≤m≤5)}\end{array}\right.$;
②当点C与抛物线顶点重合时,m=2,
此时,s=-2×22+8×2=8,
当点M与抛物线与x轴交点重合时,m=5,
此时,s=2×52-8×5=10,
∴当点M与抛物线与x轴交点重合时,△ABC的面积最大,最大面积为10.
点评 此题主要考查了二次函数的综合应用,熟练掌握待定系数法是解本题的关键.解决问题的关键是掌握运用二次函数的顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标;解题时注意分类思想的运用.


科目:初中数学 来源: 题型:解答题
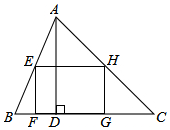 如图,△ABC的内接矩形EFGH,FG在BC上,高AD=20,BC=40,设EF=x,矩形EFGH的面积为y,试求y与x之间的函数关系式,并确定x的取值范围.
如图,△ABC的内接矩形EFGH,FG在BC上,高AD=20,BC=40,设EF=x,矩形EFGH的面积为y,试求y与x之间的函数关系式,并确定x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示的扇形统计图是某商店在第一季度里男、女服装的销售收入情况,由于二月份正值春节,男、女服装的销售收入分别比一月份增长了40%,64%,已知三月份男、女服装的销售总收入为5万元
如图所示的扇形统计图是某商店在第一季度里男、女服装的销售收入情况,由于二月份正值春节,男、女服装的销售收入分别比一月份增长了40%,64%,已知三月份男、女服装的销售总收入为5万元查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com