
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= ![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式. 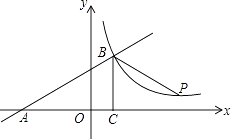
【答案】解:∵点B(2,n)、P(3n﹣4,1)在反比例函数y= ![]() (x>0)的图象上, ∴
(x>0)的图象上, ∴ ![]() .
.
解得:m=8,n=4.
∴反比例函数的表达式为y= ![]() .
.
∵m=8,n=4,
∴点B(2,4),(8,1).
过点P作PD⊥BC,垂足为D,并延长交AB与点P′.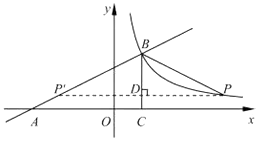
在△BDP和△BDP′中,
∴△BDP≌△BDP′.
∴DP′=DP=6.
∴点P′(﹣4,1).
将点P′(﹣4,1),B(2,4)代入直线的解析式得: ![]() ,
,
解得: ![]() .
.
∴一次函数的表达式为y= ![]() x+3
x+3
【解析】将点B(2,n)、P(3n﹣4,1)代入反比例函数的解析式可求得m、n的值,从而求得反比例函数的解析式以及点B和点P的坐标,过点P作PD⊥BC,垂足为D,并延长交AB与点P′.接下来证明△BDP≌△BDP′,从而得到点P′的坐标,最后将点P′和点B的坐标代入一次函数的解析式即可求得一次函数的表达式.


科目:初中数学 来源: 题型:
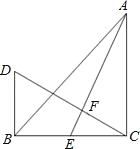
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( ) 
A.13
B.17
C.18
D.25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
(1)发现:
△CMP和△BPA是否相似,若相似给出证明,若不相似说明理由;
(2)思考:
线段AM是否存在最小值?若存在求出这个最小值,若不存在,说明理由;
(3)探究:
当△ABP≌△ADN时,求BP的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )
A.
B.
C.
D.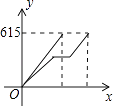
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com