
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A,B两点,抛物线y=﹣x2+bx+c过A,B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.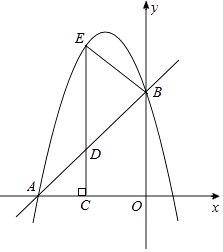
(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
【答案】
(1)解:在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,
∴A(﹣4,0),B(0,4).
∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,
∴ ![]() ,
,
解得:b=﹣3,c=4,
∴抛物线的解析式为:y=﹣x2﹣3x+4
(2)解:如图,连接AE、过点E作EF⊥y轴于点F,
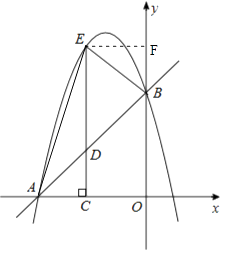
设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),
则OC=﹣m,OF=﹣m2﹣3m+4,
∵OA=OB=4,
∴BF=﹣m2﹣3m,
则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF
= ![]() ×(﹣m+4)(﹣m2﹣3m+4)﹣
×(﹣m+4)(﹣m2﹣3m+4)﹣ ![]() ×4×4﹣
×4×4﹣ ![]() ×(﹣m)×(﹣m2﹣3m).
×(﹣m)×(﹣m2﹣3m).
=﹣2m2﹣8m
=﹣2(m+2)2+8,
∵﹣4<m<0,
∴当m=﹣2时,S取得最大值,最大值为8.
即△ABE面积的最大值为8
(3)解:设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD= ![]() OC=﹣
OC=﹣ ![]() m,
m,
则D(m,4+m).
∵△ACD为等腰直角三角形,△DBE和△DAC相似
∴△DBE必为等腰直角三角形.
i)若∠BED=90°,则BE=DE,
∵BE=OC=﹣m,
∴DE=BE=﹣m,
∴CE=4+m﹣m=4,
∴E(m,4).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,
∴D(﹣3,1);
ii)若∠EBD=90°,则BE=BD=﹣ ![]() m,
m,
在等腰直角三角形EBD中,DE= ![]() BD=﹣2m,
BD=﹣2m,
∴CE=4+m﹣2m=4﹣m,
∴E(m,4﹣m).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,
∴D(﹣2,2).
综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2)
【解析】(1)根据线y=x+4与坐标轴分别交于A,B两点,得到A,B的坐标,用待定系数法求出抛物线的解析式;(2)根据题意求出点C、点E的坐标,得到S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF,求出当m=﹣2时,S取得最大值,最大值为8,得到△ABE面积的最大值为8;(3)根据题意求出点C坐标与点D坐标的关系,得到E点坐标,由点E在抛物线上,求出D点坐标,得到存在点D,使得△DBE和△DAC相似.
【考点精析】本题主要考查了相似三角形的判定的相关知识点,需要掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y1= ![]() x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣
x+b的图象l与二次函数y2=﹣x2+mx+b的图象C′都经过点B(0,1)和点C,且图象C′过点A(2﹣ ![]() ,0).
,0).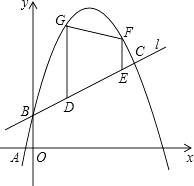
(1)求二次函数的最大值;
(2)设使y2>y1成立的x取值的所有整数和为s,若s是关于x的方程 ![]() =0的根,求a的值;
=0的根,求a的值;
(3)若点F、G在图象C′上,长度为 ![]() 的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
的线段DE在线段BC上移动,EF与DG始终平行于y轴,当四边形DEFG的面积最大时,在x轴上求点P,使PD+PE最小,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 ( )
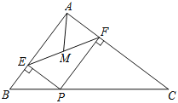
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,点M为直线AB,CD所确定的平面内的一点,若∠A105,∠M108,请直接写出∠C的度数 ;
(2)如图2,AB∥CD,点P为直线AB,CD所确定的平面内的一点,点E在直线CD上,AN平分∠PAB,射线AN的反向延长线交∠PCE的平分线于M,若∠P30,求∠AMC的度数;
(3)如图3,点P与直线AB,CD在同一平面内,AN平分∠PAB,射线AN的反向延长线交∠PCD的平分线于M,若AMC180![]() P,求证:AB∥CD.
P,求证:AB∥CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为学校购买运动会的奖品后,回学校向后勤处赵主任交账说:我买了两种书共105本,单价分别为8元和12元,买书前我领了1600元,现在还余518元.赵主任算了一下说:你肯定搞错了.
(1)赵主任为什么说他搞错了,请你用方程组的知识给予解释;
(2)王老师连忙拿出购物发票,发现的确弄错了,因为他还买了一个笔记本,但笔记本的单价已模糊不清,只能辨认出应为小于5元的整数,笔记本的单价可能为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为创建“书香校园”,购置了一批图书,已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量与购买文学类图书的数量相等.求科普类图书平均每本的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计),第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车,小聪周末到该风景区游玩,上午7:40到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林,离入口处的路程![]() (米)与时间
(米)与时间![]() (分)的函数关系如图2所示.
(分)的函数关系如图2所示.
(1)求第一班车从入口处到达塔林的时间.
(2)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变).
(3)若小聪在8:30至8:50之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过3分钟的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数( )

A. 24°B. 25°C. 30°D. 35°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com