Question

【题目】如图，一艘轮船位于灯塔B的正西方向A处，且A处与灯塔B相距60海里，轮船沿东北方向匀速航行，到达位于灯塔B的北偏东l5°方向上的C处．

(1)求∠ACB的度数；

(2)求灯塔B到C处的距离．(结果保留根号)

Answer 1

【答案】（1）30°；（2）60海里．

【解析】

（1）利用三角形内角和定理进行计算；
（2）过点B作AC的垂线，垂足为D．在△BDC中利用三角函数即可求解．

（1）在△ABC中，∠CAB=45°，∠CBA=90°+15°=105°．则∠ACB=180°-45°-105°=30°，即∠ACB=30°；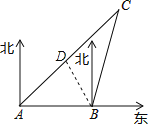

（2）过点B作AC的垂线，垂足为D，依题意可得∠DAB=45°，∠DBA=45°，AB=60海里．

AD=BD=ABsin45=60×.
在△BDC中，∠DBC=45°+15°=60°，∠BDC=90°，cos∠DBC==cos60°=．
∴BC=60（海里）．
答：灯塔B到C处的距离是60海里．