
【题目】如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,设
,设![]() 的长为
的长为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 之间的函数关系式是________.
之间的函数关系式是________.

【答案】![]()
【解析】
作DF⊥AC垂足为F点,易证△ABC≌△ADF,根据全等三角形的性质可得BC=AF,AC=DF,设BC=AF =a,则DF= AC=4BC=4a,CF=AC-AF =3a,在Rt△CDF中,由勾股定理求得a=![]() ,根据y=S△ABC+S△ACD即可求得
,根据y=S△ABC+S△ACD即可求得![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
作DF⊥AC垂足为F点,∴∠AFD=90°,
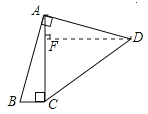
∵∠BAD=∠AFD =90°,即∠BAC+∠CAD=∠CAD+∠ADF,
∴∠BAC=∠ADF,
又∵AB=AD,∠ACB=∠AFD=90°
∴△ABC≌△ADF(AAS)
∴BC=AF,AC=DF,
设BC=AF =a,则DF= AC=4BC=4a,
CF=AC-AF =3a,
在Rt△CDF中,由勾股定理得,
CF2+DF2=CD2,即(3a)2+(4a)2=x2,
解得:a=![]() ,
,
∴y=S△ABC+S△ACD=![]() BC·AC+
BC·AC+![]() DF·AC=
DF·AC=![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知等边△ABC的两个顶点的坐标为A(-4,0),B(2,0).
(1)用尺规作图作出点C,并求出点C的坐标;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,两个三角形的顶点都在格点(网线的交点)上,下列方案中不能把△ABC平移至△DEF位置的是( )
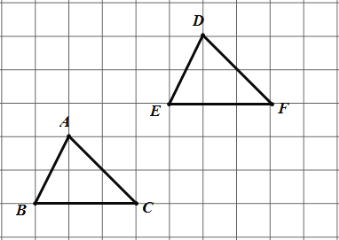
A.先把△ABC沿水平方向向右平移4个单位长度,再向上平移3个单位长度
B.先把△ABC向上平移3个单位长度,再沿水平方向向右平移4个单位长度
C.把△ABC沿BE方向移动5个单位长度
D.把△ABC沿BE方向移动6个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:x2﹣6x=(x2﹣6x+9)﹣9=(x﹣3)2﹣9;﹣x2+10=﹣(x2﹣10x+25)+25=﹣(x﹣5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
(1)按上面材料提示的方法填空:a2﹣4a= = .﹣a2+12a= = .
(2)探究:当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值?请说明理由.
(3)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数;
(2)设∠BAD=θ,
①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC平分∠BCD,AB=AD, AE⊥BC于E,AF⊥CD于F
(1)若∠ABE= 50° ,求∠CDA的度数.
(2)若AE=4,BE=2,CD=6,求四边形AECD 的面积.
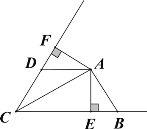
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以□ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E、F,延长BA交⊙A于G.

(1)求证:![]() .
.
(2)若![]() 的度数为70°,求∠C的度数.
的度数为70°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图②表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图像.
(1)甲、丙两地间的路程为千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x在什么范围时,高速列车离乙地的路程不超过100千米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com